Хи-квадрат распределение (Пирсона)

В связи с гауссовской теорией ошибок астроном Ф. Хельмерт исследовал суммы квадратов нормально распределенных случайных величин, придя таким образом к функции распределения Fχ_m²(x), которую позднее К. Пирсон назвал функцией распределения «хи-квадрат». Для отрицательных x функция Fχ_m²(x) = 0, а для неотрицательных x:

где m — число степеней свободы (целое положительное число),

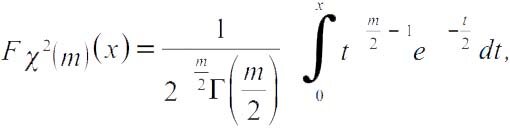
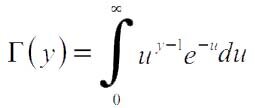значение гамма-функции Эйлера в точке y.

 

 

Соответствующая плотность вероятности задается функцией:

При m <= 2 функция плотности постоянно убывает (для x > 0), а при m > 2 имеет единственный максимум в точке x = m-2.

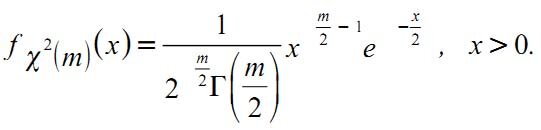
Задачи по эконометрике на распределение Пирсона смотрите тут