Гиперболические модели

Среди класса нелинейных функций, параметры которых без затруднений оцениваются методом наименьших квадратов, следует указать равностороннюю гиперболу

Такие модели могут быть использованы не только для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота, т.е. на микроэкономичеком уровне, но и на макроуровне. Классическим примером является кривая Филлипса, которая характеризуюет нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у

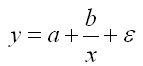
Английский экономист А. В. Филлипс, проанализировав данные более чем за 100-летний период, в конце 50-х гг. XX в. установил обратную связь процента прироста заработной платы от уровня безработицы.

Для равносторонней гиперболы вида, 1/Х заменив на z, получим линейное уравнение регрессии y = a + bz, оценка параметров которого в задачах эконометрики производится с помощью метода наименьших квадратов. Система нормальных уравнений будет выглядеть так:

Для кривой Филлипса y = 0,00679 + 0,1842/x величина параметра a, равная 0,00679, значит, что с ростом уровня безработицы темп прироста заработной платы в своем пределе стремится к нулю. Таким образом, можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю. При b < 0 имеет место медленно повышающаюся функцию с верхней асимптотой при х стремящемся в бесконечности, т.е. с максимальным предельным уровнем у, оценку которого в уравнении дает параметр а.

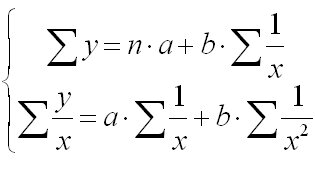
Примером гиперболической связи может также служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Математическое описание такого рода взаимосвязей получило название кривых Энгеля. В 1857 г. немецкий статистик Э. Энгель на основе анализа семейных расходов сформулировал закономерность — с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается и наоборот. Однако это увеличение не беспредельно, так как на все товары сумма долей не может превышать единицу (100%), а на отдельные непродовольственные товары этот предел может характеризоваться величиной параметра а для уравнения вида y = a — b/x, где у — доля расходов на непродовольственные товары; х — доходы (или общая сумма расходов).

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.

Суть, задачи и определения эконометрики приведены на этой странице