Проверка статистической значимости коэффициентов уравнения множественной регрессии

Построение эмпирического уравнения регрессии — начальный этап эконометрического анализа. Первое же построенное по выборке уравнение регрессии очень редко является удовлетворительным по тем или иным характеристикам. Поэтому следующей важнейшей задачей эконометрики анализа будет проверка качества уравнения регрессии. Проверка качества уравнения регрессии проводится по следующим параметрам:

• проверка статистической значимости коэффициентов регрессионного уравнения;
• проверка качества уравнения регрессии в целом;
• проверка свойств данных, выполнимость которых предполагалась при оценивании уравнения (проверка выполняемости предпосылок МНК).

Как и в случае парной регрессии, статистическая значимость коэффициентов множественной линейной регрессии с m объясняющими переменными проверяется на основе t-статистики:

имеющей в данной ситуации распределение Стьюдента с числом степеней свободы α = n — m — 1 (n — объем выборки, m — количество объясняющих переменных в модели). При требуемом уровне значимости наблюдаемое α значение t-статистики сравнивается с критической точкой t _α/2;n-m-1 распределения Стьюдента.

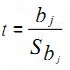
Если | t | > t _α/2;n-m-1, то коэффициент bj считается статистически значимым. В противном случае коэффициент bj считается статистически незначимым статистически близким к нулю. Это означает, что фактор Xj линейно не связан с зависимой переменной Y. Наличие этого фактора среди объясняющих переменных не оправдано со статистической точки зрения. Он не оказывает сколько-нибудь серьезного влияния на зависимую переменную, а лишь искажает реальную картину взаимосвязи. Если коэффициент bj статистически незначим, рекомендуется исключить из уравнения регрессии переменную Xj. Это не приведет к существенной потере качества модели, но сделает ее более конкретной.

Стандартную задачу по эконометрике на проверку значимости можете посмотреть на этой странице.