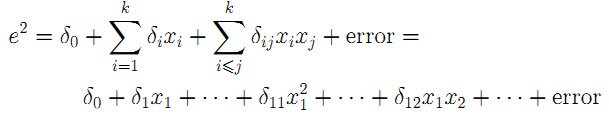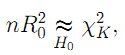Тест Уайта (White)

Этот тест применяется в том случае когда есть априор­ные предположения, что гетероскедастичность обусловлена зависимо­стью дисперсии ошибки от объясняющих переменных. В случае сто­хастических регрессоров проверяется гипотеза

H0 : Var(u/x1,…, xk) = σ²

против альтернативы

H1 : Var(u\x1,…, xk) = σ²(x1,…, xk).

В модели с детерминированными регрессорами проверяется нулевая гипотеза

H₀ :  σ₁² = σ_n²

Для проверки нулевой гипотезы White(1980) предложил следующую двухшаговую процедуру:

1. Находим OLS-остатки ei в исходной модели регрессии;
2. Вычисляем коэффициент R₀² во вспомогательной регрессии е² на константу, регрессоры, их квадраты и попарные произведения:

При справедливости нулевой гипотезы о гомоскедастичности ошибок статистика nR₀² для проверки значимости вспомогательной регрессии «в целом» асимптотически (т.е. при больших объемах выборки) имеет распределение хи-квадрат

где число степеней свободы К равно числу регрессоров во вспомо­гательной регрессии. Таким образом, при заданном уровне зна­чимости α (асимптотически) нулевая гипотеза о гомоскедастичности отвергается при nR₀² > χ²кр, где критическое значение χ²_кр = χ²(α ; К). Несложно показать, что К = (k² + 3k)/2, где k, как обычно, число регрессоров в исходной модели регрессии.

Замечание. Важно отметить, что вспомогательная регрессия не имеет никакой экономической интерпретации, а нужна только для вычисления коэффициента R₀².

Тест White является наиболее общим тестом для проверки гетероскедастичности ошибки регрессии, однако он имеет следующие недо­статки:

• даже при небольшом количестве регрессоров в исходной модели во вспомогательной модели, оцениваемой на втором шаге, может быть «много» (относительно объема выборки) оцениваемых ко­эффициентов, что уменьшает мощность теста;
• если нулевая гипотеза отвергается, то не дается указаний на функциональную форму гетероскедастичности (на вид функции σ²(х)).
• тест не учитывает зависимость дисперсии ошибок от невключенных в модель регрессоров

Замечание. Для проверки значимости вспомогательной регрессии «в целом» также можно использовать F-статистику, асимптотически имеющую распределение Фишера.

Если во вспомогательной модели «много» (относительно объ­ема выборки) коэффициентов, то можно воспользоваться следующей модификацией теста White:

1. находим остатки ei и предсказанные значения yi в исходной модели регрессии;
2. оцениваем вспомогательную регрессию e²  на yi^ и y²i^

находим коэффициента R₀².

При справедливости нулевой гипотезы о гомоскедастичности ошибок статистика пR₀²  для проверки значимости вспомогательной регрессии «в целом» асимптотически (т.е. при больших объемах выборки) имеет распределение хи-квадрат

Таким образом, при заданном уровне значимости α (асимптотически) нулевая гипотеза о гомоскедастичности отвергается при nR₀² > χ²кр , где критическое значение χ²_кр = χ²(α ;2).