Сезонная составляющая (сезонная компонента) и её оценка.
Известны данные по ВВП в России за 2008-2012 г.
|
год |
квартал |
объём ВВП, млрд.руб |
|
2008 |
1 |
8878 |
|
2 |
10238 |
|
|
3 |
11542 |
|
|
4 |
10619 |
|
|
2009 |
1 |
8335 |
|
2 |
9245 |
|
|
3 |
10411 |
|
|
4 |
10816 |
|
|
2010 |
1 |
9617 |
|
2 |
10693 |
|
|
3 |
11843 |
|
|
4 |
13019 |
|
|
2011 |
1 |
11680 |
|
2 |
13038 |
|
|
3 |
14406 |
|
|
4 |
15462 |
Построить аддитивную модель временного ряда, выделив сезонную и трендовую составляющие
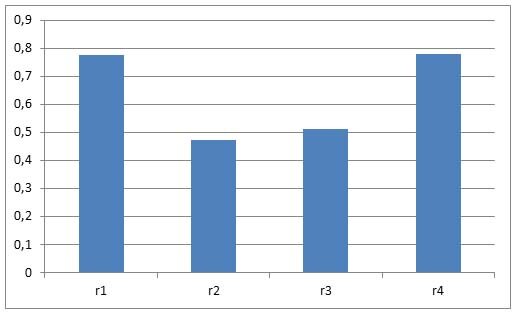
Найдём коэффициенты автокорреляции
| r1 |
0,777705 |
| r2 |
0,475503 |
| r3 |
0,513819 |
| r4 |
0,781028 |
Построим коррелограмму
По высоким значениям коэффициентов автокорреляции 1 и 4 порядка выдвигаем гипотезу о наличии тренда и сезонной составляющей .
Для оценки сезонной компоненты аддитивной модели составим таблицу
Для этого:
- Просуммируем уровни ряда последовательно за 4 квартала со сдвигом на один сезон (итого за 4 квартала)
- Найдем скользящие средние, делением каждой суммы на 4.
- Приведем скользящие средние с помощью центрирования, найдя средние значения из двух последовательных скользящих средних.
- Найдем оценки сезонной компоненты как разность между фактическим y и центрированной скользящей средней
|
t |
y |
Итого за 4 кв. |
Скользящая средняя за 4 кв. |
Центрированная скользящая средняя |
Оценка сезонной компоненты |
|
1 |
8878 |
— |
— |
— |
— |
|
2 |
10238 |
41277 |
10319,3 |
— |
— |
|
3 |
11542 |
40734 |
10183,5 |
10251,38 |
1290,63 |
|
4 |
10619 |
39741 |
9935,3 |
10059,38 |
559,63 |
|
5 |
8335 |
38610 |
9652,5 |
9793,88 |
-1458,88 |
|
6 |
9245 |
38807 |
9701,8 |
9677,13 |
-432,13 |
|
7 |
10411 |
40089 |
10022,3 |
9862,00 |
549,00 |
|
8 |
10816 |
41537 |
10384,3 |
10203,25 |
612,75 |
|
9 |
9617 |
42969 |
10742,3 |
10563,25 |
-946,25 |
|
10 |
10693 |
45172 |
11293,0 |
11017,63 |
-324,63 |
|
11 |
11843 |
47235 |
11808,8 |
11550,88 |
292,13 |
|
12 |
13019 |
49580 |
12395,0 |
12101,88 |
917,13 |
|
13 |
11680 |
52143 |
13035,8 |
12715,38 |
-1035,38 |
|
14 |
13038 |
54586 |
13646,5 |
13341,13 |
-303,13 |
|
15 |
14406 |
— |
— |
— |
— |
|
16 |
15462 |
— |
— |
— |
— |
Рассчитаем значения сезонной компоненты
|
Показатели |
Год |
Квартал |
|||
|
1 кв. |
2 кв. |
3 кв. |
4 кв. |
||
|
1 |
1290,63 |
559,63 |
|||
|
2 |
-1458,88 |
-432,13 |
549,00 |
612,75 |
|
|
3 |
-946,25 |
-324,63 |
292,13 |
917,13 |
|
|
4 |
-1035,38 |
-303,13 |
|||
| Итого за сезон |
-3440,50 |
-1059,88 |
2131,75 |
2089,50 |
|
| Средняя оценка сезонной компоненты, |
-1146,83 |
-353,29 |
710,58 |
696,50 |
|
| Скорректированная сезонная компонента, |
-1123,57 |
-330,03 |
733,84 |
719,76 |
|
Все значения для расчетов возьмем из колонки «Оценка сезонной компоненты», последовательно внося их в таблицу
Сумма «Скорректированной сезонной компоненты» равна нулю.
Для расчета скорректированной сезонной компоненты определим корректирующий коэффициент.
Составим таблицу, где T + ε колонка с возможным трендом (за вычетом сезонности)
|
t |
y |
Si (скорректированная S) |
y – S = T + ε |
|
1 |
2301 |
-373,48 |
2674,48 |
|
2 |
2567 |
-139,52 |
2706,52 |
|
3 |
3050 |
266,48 |
2783,52 |
|
4 |
3064 |
246,52 |
2817,48 |
|
5 |
2891 |
-373,48 |
3264,48 |
|
6 |
3149 |
-139,52 |
3288,52 |
|
7 |
3671 |
266,48 |
3404,52 |
|
8 |
3696 |
246,52 |
3449,48 |
|
9 |
3522 |
-373,48 |
3895,48 |
|
10 |
3984 |
-139,52 |
4123,52 |
|
11 |
4645 |
266,48 |
4378,52 |
|
12 |
4979 |
246,52 |
4732,48 |
|
13 |
4441 |
-373,48 |
4814,48 |
|
14 |
5070 |
-139,52 |
5209,52 |
|
15 |
5897 |
266,48 |
5630,52 |
|
16 |
6354 |
246,52 |
6107,48 |
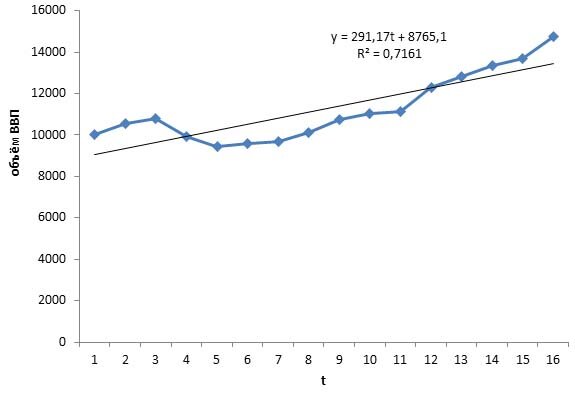
Строим график модели за вычетом сезонной компоненты
Коэффициенту детерминации очень высок (близок к 1), таким образом, полученная линейная модель может использоваться для прогнозирования
Оценим качество такой модели с помощью инструмента регрессия
| ВЫВОД ИТОГОВ | ||||
|
Регрессионная статистика |
||||
| Множественный R |
0,846 |
|||
| R-квадрат |
0,716 |
|||
| Нормированный R-квадрат |
0,696 |
|||
| Стандартная ошибка |
903,55 |
|||
| Наблюдения |
16 |
|||
| Дисперсионный анализ | ||||
|
|
df |
SS |
MS |
F |
| Регрессия |
1 |
28826034 |
28826034 |
35,30883 |
| Остаток |
14 |
11429564 |
816397,4 |
|
| Итого |
15 |
40255598 |
||
|
|
Коэффи-циенты |
Стандартная ошибка |
t-статистика |
P-Значение |
| Y-пересечение |
8765,144 |
473,824 |
18,499 |
3,09E-11 |
| t |
291,174 |
49,002 |
5,942 |
3,6E-05 |
Модель y = 291,174t + 8765,144 высокого качества, поскольку коэффициент корреляции очень высок и модель значима в целом и по параметрам при уровне значимости 95%, т.к. уровни значимости критерия Фишера и Стьюдента намного меньше 5% (0,05) – см. колонки Значимость F и P-Значение.