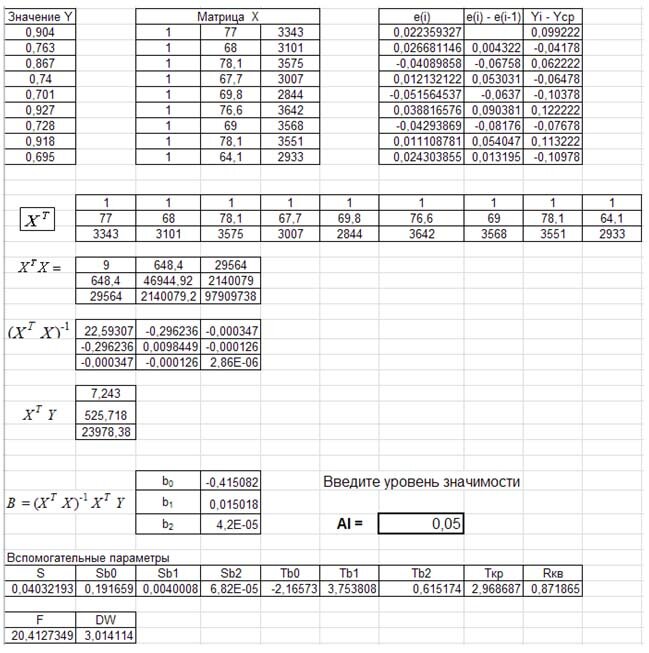
Анализ уравнения множественной регрессия матричным способом
Представим данные наблюдений в матричной форме
|
Значение Y |
Матрица Х |
||
|
0,904 |
1 |
77 |
3343 |
|
0,763 |
1 |
68 |
3101 |
|
0,867 |
1 |
78,1 |
3575 |
|
0,74 |
1 |
67,7 |
3007 |
|
0,701 |
1 |
69,8 |
2844 |
|
0,927 |
1 |
76,6 |
3642 |
|
0,728 |
1 |
69 |
3568 |
|
0,918 |
1 |
78,1 |
3551 |
|
0,695 |
1 |
64,1 |
2933 |
|
1200 |
1 |
5675 |
3,4 |
|
1357 |
1 |
7100 |
3,6 |
|
1516 |
1 |
9206 |
3,6 |
Найдем параметры модели
B = (XT X)-1 XT Y .
Проведем транспонирование матрицы с помощью функции ТРАНСП, получим
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
77 |
68 |
78,1 |
67,7 |
69,8 |
76,6 |
69 |
78,1 |
64,1 |
|
3343 |
3101 |
3575 |
3007 |
2844 |
3642 |
3568 |
3551 |
2933 |
Умножим матрицу XT и X с помощью функции МУМНОЖ
|
9 |
648,4 |
29564 |
|
648,4 |
46944,92 |
2140079 |
|
29564 |
2140079,2 |
97909738 |
Обратим матрицу XT X с помощью функции МОБР
(XT X)-1
| 22,59307 | -0,296236 | -0,000347 |
| -0,296236 | 0,0098449 | -0,000126 |
| -0,000347 | -0,000126 | 2,86E-06 |
Умножим матрицу XT и Y с помощью функции МУМНОЖ
|
7,243 |
|
525,718 |
|
23978,38 |
Умножим матрицу (XT X)-1 на XTY получим коэффициенты уравнения регрессии.
|
b0 |
-0,415082 |
|
b1 |
0,015018 |
|
b2 |
4,2E-05 |
Остальные расчеты представим ниже
Пояснения: Для вычисления дисперсий параметров необходимо вычислить S2 в соответствие. На основании Т-статистик делается вывод о значимости коэффициентов регрессии их доверительные интервалы. Значения tкр можно получить, используя статистическую функцию СТЬЮДРАСПОБР. По соответствующим формулам вычисляются коэффициент детерминации R2 и F – критерий, на основании которых делается вывод о значимости уравнения регрессии в целом. Для нахождения критической точки fкр нужно воспользоваться функцией FРАСПОБР
Расчетные значения, полученные по формулам, совпадают с расчетами в Excel. Задание выполнено верно.