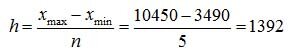Группировка. Формула Стерджесса
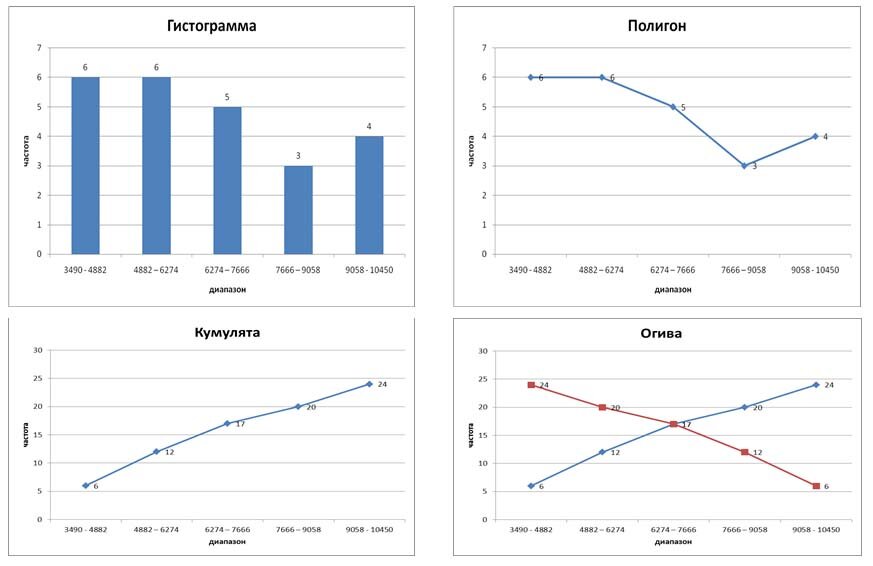
Провести группировку жителей поселка по доходу с равными интервалами и оптимальным числом групп и представить полученные данные в виде статистического ряда распределения и гистограммы. На основе гистограммы построить полигон, кумуляту и огиву распределения жителей поселка по доходу.
|
№ |
Дох. |
№ |
Дох. |
|
1 |
3820 |
13 |
6660 |
|
2 |
9470 |
14 |
5490 |
|
3 |
3490 |
15 |
5980 |
|
4 |
7790 |
16 |
6250 |
|
5 |
4210 |
17 |
8390 |
|
6 |
3870 |
18 |
3630 |
|
7 |
4490 |
19 |
6090 |
|
8 |
9620 |
20 |
10450 |
|
9 |
6200 |
21 |
6800 |
|
10 |
6350 |
22 |
6470 |
|
11 |
7430 |
23 |
9160 |
|
12 |
7670 |
24 |
5110 |
Определяем число групп по формуле Стерджесса:
n = 1 + 3,322lgN = 1 + 3,322lg24 = 5,6
принимаем n = 5
Определяем шаг интервала:
Xmax, Xmin- максимальное и минимальное значение
n – число групп
Произведем группировку с равными интервалами
|
Интервалы |
Диапазон |
частота, f |
Накопленная частота, f |
|
1 |
3490 — 4882 |
6 |
6 |
|
2 |
4882 – 6274 |
6 |
12 |
|
3 |
6274 – 7666 |
5 |
17 |
|
4 |
7666 – 9058 |
3 |
20 |
|
5 |
9058 — 10450 |
4 |
24 |
Гистограмма. Полигон. Кумулята. Огива
Если Вас интересуют задачи по статистике заходите сюда.