Коэффициент корреляции и коэффициент детерминации
Эмпирический коэффициент детерминации
Эмпирический коэффициент детерминации широко используется в задачах статистики и является показателем, который представляет долю межгруппопой дисперсии в общей дисперсии результативного признака и характеризует силу влияния группировочного признака на образование общей вариации. Он может быть рассчитан по формуле:
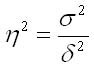
Данный коэффициент показывает долю вариации результативного признака у под влиянием фактора х. При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной сильной связи — единице.
Эмпирическое корреляционное отношение
Эмпирическое корреляционное отношение представляется как корень квадратный из эмпирического коэффициента детерминации. Оно показывает тесноту связи между статистическими данными и определяется по формуле:
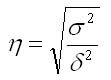
где числитель — дисперсия групповых средних;
знаменатель — общая дисперсия.
Корреляционное отношение равно нулю, если связи между данными нет. В таком случае все групповые средние будут равны между собой и межгрупповой вариации не будет.
Корреляционное отношение равно единице тогда, когда связь функциональная. В этом случае дисперсия групповых средних будет равна общей дисперсии, т. е. внутригрупповой вариации не будет.
Чем значения корреляционного отношения ближе к единице, тем сильнее, ближе к функциональной зависимости связь между признаками.
Критерий Пирсона
Критерий Пирсона вычисляется по формуле:
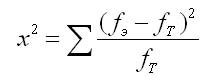
где fэ и fт — эмпирические и теоретические частоты.
С помощью критерия Пирсона по таблицам определяют вероятность P(х^2). Входами в таблицу являются значения х^2 и число степеней свободы k = n — р -1.
Если Р > 0,05, то считается, что эмпирические и теоретические распределения близки. При Р принадлежащим [0,02; 0,05] совпадение между ними удовлетворительное, а в других случаях — недостаточное.
Коэффициент асимметрии
Коэффициент асимметрии рассчитывается по формуле:
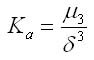
где числитель — центральный момент третьего порядка.
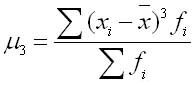
б^3 — куб среднего квадратичного отклонения.
Коэффициент асимметрии является безмерной величиной, что позволяет использовать его для различных распределений. При левосторонней асимметрии Mо > Mt > xср, при правосторонней — обратные соотношения. Это позволяет применять наиболее простой показатель асимметрии:
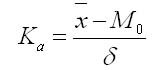
Эксцесс в статистике
Эксцесс есть степень крутости эмпирического распределения по отношению к нормальному. Он определяется по формуле:
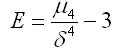
где числитель — центральный момент четвертого порядка
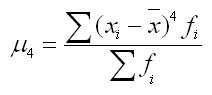
Когда распределение островершинное по отношению к нормальному, эксцесс будет положительным, если плосковершинное — отрицательным. Для нормального распределения Е = 0.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.