Нелинейные модели
Нелинейные модели, являющиеся линейными относительно параметров, сводятся к линейным простой заменой переменных. Нелинейные модели, которые сводятся к линейным после некоторых преобразований с последующей заменой переменных, называются внутренне линейными. Нелинейные модели, которые нельзя преобразовать к линейной форме, называются внутренне нелинейными. С помощью t- и F-статистики исследуют линеаризованную модель.
Примеры исследования нелинейных моделей
Пример расчета параметров нелинейных моделей
Выбор формы нелинейной модели
Многообразие и сложность экономических процессов предопределяет многообразие моделей, используемых для эконометрического анализа. Это существенно усложняет процесс нахождения максимально адекватной формулы зависимости. Для случая парной регрессии подбор модели обычно осуществляется по виду расположения наблюдаемых точек на корреляционном поле. Однако нередки ситуации, когда расположение точек приблизительно соответствует нескольким функциям и необходимо из них выявить наилучшую. Еще более неоднозначна ситуация для множественной регрессии, так как наглядное представление статистических данных в этом случае невозможно.
На практике неизвестно, какая модель является верной, и зачастую подбирают такую, которая наиболее точно соответствует реальным данным. При этом необходимо учитывать, что идеальной модели не существует. Поэтому, чтобы выбрать качественную модель, необходимо ответить на ряд вопросов, возникающих при ее анализе.
Обычно выделяют следующие признаки «хорошей» модели.
- Скупость (простота). Из двух моделей, приблизительно одинаково отражающих реальность, предпочтение отдается содержащей меньшее число объясняющих переменных.
- Единственность. Для любого набора статистических данных определяемые коэффициенты должны вычисляться однозначно.
- Максимальное соответствие. Уравнение тем лучше, чем большую часть разброса зависимой переменной оно может объяснить. Поэтому стремятся построить уравнение с максимально возможным скорректированным коэффициентом детерминации R2.
- Согласованность с теорией. Никакое уравнение не может быть признано качественным, если оно не соответствует известным теоретическим предпосылкам. Вообще говоря, теория тоже может оказаться ошибочной.
- Прогнозные качества. Модель может быть признана качественной, если полученные на ее основе прогнозы подтверждаются реальностью.
- Другим критерием прогнозных качеств оцененной модели регрессии может служить следующее отношение: V = S/yср, где S — стандартная ошибка регрессии, y — среднее значение зависимой переменной уравнения регрессии. Если величина V мала (а она определяет относительную ошибку прогноза в процентах) и отсутствует автокорреляция остатков (определяемая по величине статистики DW Дарбина-Уотсона), то прогнозные качества модели высоки.
Если уравнение регрессии используется для прогнозирования, то величина V обычно рассчитывается не для того периода, на котором оценивалось уравнение, а для некоторого следующего за ним временного интервала, для которого известны значения зависимой и объясняющих переменных. Тем самым на практике проверяются прогнозные качества модели. В случае положительного решения, если можно спрогнозировать значения объясняющих переменных на некоторый последующий период, построенная модель обоснованно может быть использована для прогноза значений объясняемой переменной Y. Следует помнить, что период прогнозирования должен быть, по крайней мере, в три раза короче периода, по которому оценивалось уравнение регрессии.
Рассмотрим виды ошибок спецификации. Одним из базовых предположений построения качественной модели является правильная (хорошая) спецификация уравнения регрессии. Правильная спецификация уравнения регрессии означает, что оно в целом верно, отражает соотношение между экономическими показателями, участвующими в модели. Это является необходимой предпосылкой дальнейшего качественного оценивания.
Неправильный выбор функциональной формы или набора объясняющих переменных называется ошибками спецификации. Рассмотрим основные типы ошибок спецификации.
Ошибки спецификации
- Отбрасывание значимой переменной. Последствия данной ошибки достаточно серьезны. Оценки, полученные с помощью МНК, являются смещенными и несостоятельными даже при бесконечно большом числе испытаний. Следовательно, возможные интервальные оценки и результаты проверки соответствующих гипотез будут ненадежными.
- Добавление незначимой переменной. В некоторых случаях в уравнения регрессии включают слишком много объясняющих переменных, причем не всегда обоснованно. Последствия данной ошибки будут не столь серьезными, как в предыдущем случае. Оценки коэффициентов модели остаются, как правило, несмещенными и состоятельными. Однако их точность уменьшается, увеличивая при этом стандартные ошибки, т. е. оценки становятся неэффективными, что отразится на их устойчивости.
- Выбор неправильной функциональной формы. Последствия такой ошибки будут весьма серьезными. Обычно ошибка приводит либо к получению смещенных оценок, либо к ухудшению статистических свойств оценок коэффициентов регрессии и других показателей качества уравнения. В первую очередь это связано с нарушением условий Гаусса-Маркова для отклонений. Прогнозные качества модели в этом случае очень низки.
Обнаружение и корректировка ошибок спецификации
При построении уравнений регрессии, особенно на начальных этапах, ошибки спецификации весьма нередки. Они допускаются обычно из-за поверхностных знаний об исследуемых экономических процессах либо из-за недостаточно глубоко проработанной теории, или из-за погрешностей сбора и обработки статистических данных при построении эмпирического уравнения регрессии. Важно уметь обнаружить и исправить эти ошибки. Сложность процедуры определяется типом ошибки и нашими знаниями об исследуемом объекте.
Если в уравнении регрессии имеется одна несущественная переменная, то она обнаружит себя по низкой t-статистике. В дальнейшем эту переменную исключают из рассмотрения.
Если в уравнении несколько статистически незначимых объясняющих переменных, то следует построить другое уравнение регрессии без этих незначимых переменных. Затем с помощью F-статистики
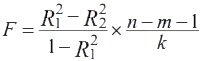
При наличии нескольких несущественных переменных, возможно, имеет место мультиколлинеарность. Рекомендуемые выходы из этой ситуации подробно рассмотрены ранее.
Однако осуществление указанных проверок имеет смысл лишь при правильном подборе вида (функциональной формы) уравнения регрессии, что можно осуществить, если согласовывать его с теорией.
Отметим, что выбор модели далеко не всегда осуществляется однозначно, и в дальнейшем требуется сравнивать модель как с теоретическими, так и с эмпирическими данными, совершенствовать ее. Напомним, что при определении качества модели обычно анализируются следующие параметры:
- скорректированный коэффициент детерминации R2;
- t-статистики;
- критерий Дарбина-Уотсона (DW);
- согласованность знаков коэффициентов с теорией;
- прогнозные качества (ошибки) модели.
Если все эти показатели удовлетворительны, то данная модель может быть предложена для описания исследуемого реального процесса. Если же какая-либо из описанных выше характеристик не является удовлетворительной, то есть основания сомневаться в качестве данной модели (неправильно выбрана функциональная форма уравнения; не учтена важная объясняющая переменная; имеется объясняющая переменная, не оказывающая значимого влияния на зависимую переменную).
Для более детального анализа адекватности модели может быть предложено исследование остаточного члена модели.
Исследование остаточного члена модели
Графическое представление поведения остаточного члена e (т. е. графическое представление случайных отклонений ei, (i = 1, 2,…, n) позволяет, прежде всего, проанализировать наличие автокорреляции и гетероскедастичности (непостоянства дисперсий отклонений). Кроме того, с помощью графического представления отклонений ei может быть также обнаружена неправильная спецификация уравнения. Для этого строится график зависимости величин отклонений ei от номера наблюдения i.
Если зависимость, изображенная на этом графике, имеет регулярный (неслучайный) характер, то это означает, что исследуемое уравнение регрессии неверно специфицировано.
Существует и ряд других тестов обнаружения ошибок спецификации, среди которых можно выделить:
- Тест Рамсея RESET (Regression specification error test).
- Тест (критерий) максимального правдоподобия (The Likeli¬hood Ratio test).
- Тест Валда (The Wald test).
- Тест множителя Лагранжа (The Lagrange multiplier test).
- Тест Хаусмана (The Hausman test).
- Преобразование Бокса-Кокса (Box–Cox transformation).
Подробное описание данных тестов выходит за рамки вводного курса. Отметим, что суть указанных тестов состоит либо в осуществлении преобразований случайных отклонений, либо в масштабировании зависимой переменной, с тем чтобы можно было сравнить начальное и преобразованное уравнения регрессии на основе известного критерия.
Стандартная схема анализа зависимостей состоит в осуществлении ряда последовательных процедур.
- Подбор начальной модели осуществляется на основе экономической теории, предыдущих знаний об объекте исследования, опыта исследователя и его интуиции.
- Оценка параметров модели на основе имеющихся статистических данных.
- Осуществление тестов проверки качества модели (обычно используются t-статистики для коэффициентов регрессии, F-статистика для коэффициента детерминации, статистика Дарбина-Уотсона для анализа отклонений и ряд других тестов).
- При наличии хотя бы одного неудовлетворительного ответа по какому-либо тесту модель совершенствуется с целью устране¬ния выявленного недостатка.
- При положительных ответах по всем проведенным тестам модель считается качественной. Она используется для анализа и прогноза объясняемой переменной.
Однако необходимо предостеречь от абсолютизации полученного результата, поскольку даже качественная модель является подгонкой спецификации модели под имеющийся набор данных.
Одно из главных направлений эконометрического анализа — постоянное совершенствование моделей. Совершенной модели не существует. В силу постоянно изменяющихся условий протекания экономических процессов не может быть и постоянно качественных моделей. Новые условия требуют пересмотра даже весьма устойчивых моделей.
Достаточно спорным является вопрос, как строить модели: а) начинать с самой простой и постоянно усложнять ее; б) начинать с максимально сложной модели и упрощать ее на основе проводимых исследований.
Оба подхода имеют как достоинства, так и недостатки. Например, если следовать схеме (а), то происходит обыкновенная подгонка модели под эмпирические данные. При теоретически более оправданном подходе (б) поиск возможных направлений совершенствования модели зачастую сводится к полному перебору, что делает проводимый анализ неэффективным. На этапах упрощения модели возможно также отбрасывание объясняющих переменных, которые были бы весьма полезны в упрощенной модели. Итак, построение модели является индивидуальным в каждой конкретной ситуации и опирается на серьезные знания экономической теории и статистического анализа.
Однако отметим, что при всех недостатках моделей принятие на их основе решений приводит в целом к гораздо более точным результатам, чем при принятии решений лишь на основе интуиции и экономической теории.
Перейти на страницу решения контрольных по эконометрке можно тут