Средние ошибки повторной и бесповторной выборки
Средняя ошибка выборки
Средняя ошибка выборки представляет из себя такое расхождение между средними выборочной и генеральной совокупностями, которое не превышает ±б (дельта).
На основании теоремы Чебышева П. Л. величина средней ошибки при случайном повторном отборе в контрольных работах по статистике рассчитывается по формуле (для среднего количественного признака):
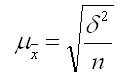
где числитель — дисперсия признака х в выборочной совокупности;
n — численность выборочной совокупности.
Для альтернативного признака формула средней ошибки выборки для доли по теореме Я. Бернулли рассчитывается по формуле:
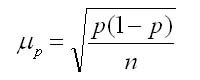
где р(1- р) — дисперсия доли признака в генеральной совокупности;
n — объем выборки.
Вследствие, того что дисперсия признака в генеральной совокупности точно не известна, на практике используют значение дисперсии, которое рассчитано для выборочной совокупности на основании закона больших чисел. Согласно данному закону выборочная совокупность при большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности.
Поэтому расчетные формулы средней ошибки при случайном повторном отборе будут выглядеть таким образом:
1. Для среднего количественного признака:
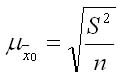
где S^2 — дисперсия признака х в выборочной совокупности;
n — объем выборки.
2. Для доли (альтернативного признака):
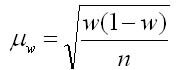
где w (1 — w) — дисперсия доли изучаемого признака в выборочной совокупности.
В теории вероятностей было показано, что генеральная дисперсия выражается через выборочную согласно формуле:
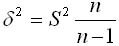
В случаях малой выборки, когда её объем меньше 30, необходимо учитывать коэффициент n/(n-1). Тогда среднюю ошибку малой выборки рассчитывают по формуле:
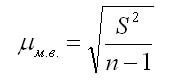
Так как в процессе бесповторной выборки сокращается численность единиц генеральной совокупности, то в представленных выше формулах расчета средних ошибок выборки нужно подкоренное выражение умножить на 1- (n/N).
Расчетные формулы для такого вида выборки будут выглядеть так:
1. Для средней количественного признака:
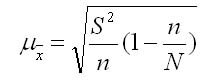
где N — объем генеральной совокупности; n — объем выборки.
2. Для доли (альтернативного признака):
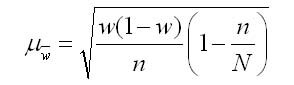
где 1- (n/N) — доля единиц генеральной совокупности, не попавших в выборку.
Поскольку n всегда меньше N, то дополнительный множитель 1 — (n/N) всегда будет меньше единицы. Это означает, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. Когда доля единиц генеральной совокупности, которые не попали в выборку, существенная, то величина 1 — (n/N) близка к единице и тогда расчет средней ошибки производится по общей формуле.
Средняя ошибка зависит от следующих факторов:
1. При выполнении принципа случайного отбора средняя ошибка выборки определяется во-первых объемом выборки: чем больше численность, тем меньше величины средней ошибки выборки. Генеральная совокупность характеризуется точнее тогда, когда больше единиц данной совокупности охватывает выборочное наблюдение
2. Средняя ошибка также зависит от степени варьирования признака. Степень варьирования характеризуется дисперсией. Чем меньше вариация признака (дисперсия), тем меньше средняя ошибка выборки. При нулевой дисперсии (признак не варьируется) средняя ошибка выборки равна нулю, таким образом, любая единица генеральной совокупности будет характеризовать всю совокупность по этому признаку.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.