Средняя арифметическая, её виды
Понятие средней арифметической
Средняя арифметическая — такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий объем импорта за год — это сумма импорта, деленная на 12 месяцев.
Средняя арифметическая может быть вычислена по формуле:
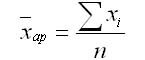
где n — численность совокупности (или число месяцев).
Например, суммарный объем импорта в 2013 году составил 314967 млн. долл. Для нахождения этой величины мы просуммировали данные по месяцам
| Месяц | Импорт |
| Январь | 19806,1 |
| Февраль | 24632,8 |
| Март | 26608,7 |
| Апрель | 28195,9 |
| Май | 24326,4 |
| Июнь | 26097,8 |
| Июль | 28023,7 |
| Август | 25987,2 |
| Сентябрь | 26263,1 |
| Октябрь | 28098,4 |
| Ноябрь | 27193,3 |
| Декабрь | 29733,7 |
| Сумма | 314967,0 |
Средняя арифметическая находится так: 314967 : 12 = 26247,3 млн. долл. (12 — число месяцев)
Смотрите видео по нахождению средней арифметической величины
Виды средней арифметической величины
Средняя арифметическая величина используется в форме простой средней и взвешенной средней. Средняя арифметическая простая равна простой сумме отдельно взятых значений осредняемого признака, разделенная на общее число этих значений. В различных контрольных по статистике она используется тогда, когда имеются несгруппированные индивидуальные значения признака, и может быть вычислена по формуле:
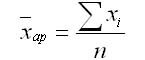
где n — общая численность совокупности значений х.
Средняя арифметическая взвешенная — это средняя из вариантов, которые повторяются разное число раз или имеют различный вес. Она может быть рассчитана по формуле:
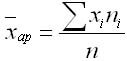
Основные свойства средней арифметической
- Если индивидуальные значения признака (варианты), уменьшить (увеличить) в n раз, то среднее значение нового признака соответственно уменьшится или увеличится во столько же.
- Если все варианты осредняемого признака уменьшить (увеличить) на число А, то средняя арифметическая соответственно изменится на это же число.
- Если вес всех осредняемых вариантов уменьшить (увеличить) в k раз, то средняя арифметическая не изменится.
- Сумма отклонений отдельных значений признака от средней арифметической равна нулю.
Часто приходится вычислять среднюю по групповым средним или по средним отдельных частей совокупности. Например, средняя рождаемость в стране представляет собой среднее из средних рождаемости по отдельным регионам страны. Средние из средних определяются так же, как и средние из первоначальных значений признака.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.