Средние величины, средняя арифметическая и средняя гармоническая
Понятие средней величины
Средней величиной признака Х некоторой статистической совокупности называется обобщающий показатель и он характеризует типичный уровень явления в конкретных условиях времени и места, а также отражает величину варьирующего признака в расчете на единицу качественно однородной совокупности. Она определяет характерный уровень изучаемых явлений, характеризует эти уровни и их изменения во времени и пространстве.
Любая средняя величина характеризует изучаемую совокупность по одному признаку, но для характеристики любой совокупности, описания ее типичных черт и качественных особенностей применяют систему средних показателей. Средняя величина должна вычисляться с учетом экономического содержания исследуемого показателя.
В большинстве контрольных статистики средняя величина путем отношения объема признака к числу явлений, обладающих этим признаком. Среди основных направлений применения средних величин можно выделить следующие: характеристика уровня развития явления, характеристика изменения уровня явлений по времени, сравнение двух или нескольких уровней, производство прогнозных расчетов и расценок, выявление и характеристика связей явлений и т. д.
Понятие среднего показателя
Средний показатель показывает то общее, что характерно для всех единиц изучаемой совокупности, но в то же время игнорирует различия отдельных единиц. Вычисление среднего показателя — один из распространенных приемов обобщения. Он характеризует всю совокупность явлений, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях.
Виды средних величин
Существуют различные виды средних величин, но наиболее часто применяются четыре: средняя арифметическая, средняя гармоническая, средняя квадратичная и средняя геометрическая. Выбор вида средней величины определяется экономическим содержанием какого-либо показателя и исходных данных, а также путем конкретного анализа изучаемой совокупности, материальным содержанием изучаемого явления и принципами суммирования и взвешивания.
Перечисленные виды средних величин можно объединить общей формулой (среднее значение исследуемого явления):
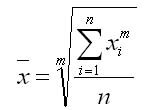
m — показатель степени средней величины;х — текущее значение осредняемого признака;
n — число признаков.
В зависимости от значения показателя степени m различают следующие виды степенных средних величин, если:
m = -1 — средняя гармоническая;
m = 0 — средняя геометрическая;
m = 1 — средняя арифметическая;
m = 2 — средняя квадратичная.
В экономике используется большое количество показателей, вычисляемых в виде средних величин. Например, интегральным показателем доходов работающих акционерного общества (АО) служит средний доход одного рабочего, который определяется отношением суммарного фонда заработной платы и выплат социального характера за определенный период (год, квартал, месяц) к итоговой численности рабочих АО.
Для рабочих с одинаковым уровнем доходов, например, работников бюджетной сферы и пенсионеров по старости можно определить доли расходов на покупку продуктов питания. Так можно расчитать среднюю продолжительность рабочего дня, средний тарифный разряд рабочих, средний уровень производительности труда и т.д.
Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.