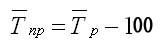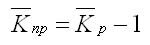Средние показатели динамики: уровень ряда, абсолютный прирост, темп роста

Средний уровень ряда в статистике

Средний уровень ряда определяет обобщенную величину абсолютных уровней. Он определяется по средней, исчисленной из значений, меняющихся во времени. Методы расчета среднего уровня интервального и моментного рядов динамики разные.

Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической:

1. При равных интервалах используют среднюю арифметическую простую:

где у — абсолютные уровни ряда;

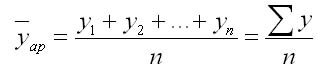
n — число уровней ряда.

2. При неравных интервалах используют среднюю арифметическую взвешенную:

где у1,…,уn — уровни ряда динамики;

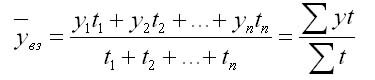
t1,… tn — веса, длительность интервалов времени.

Средний уровень моментного ряда динамики рассчитывается по формуле:

1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда:

где у1,…,уn — уровни периода, за который делается расчет;
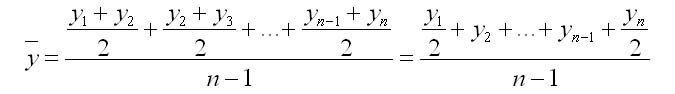
n — число уровней;
n-1 — длительность периода времени.

2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной:

где у1,…,уn — уровни рядов динамики;
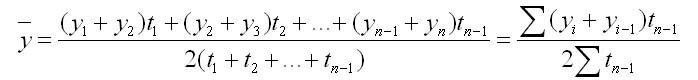
t — интервал времени между смежными уровнями

Средний абсолютный прирост в задачах статистики

Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам:

1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую:

где n — число степенных абсолютных приростов в исследуемом периоде.

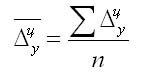
2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов

где m — число уровней ряда динамики в исследуемом периоде, включая базисный.

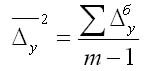
Средний темп роста

Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.

В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую.

Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»:

где n — число цепных коэффициентов роста;
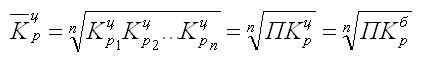
Кц — цепные коэффициенты роста;
Кб — базисный коэффициент роста за весь период.

Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста.

Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая:

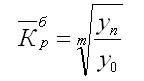
Средний темп прироста

Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%:

Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу.

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.