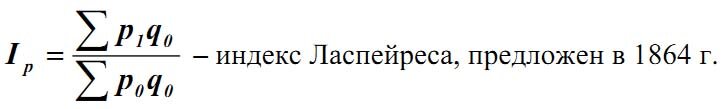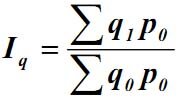Общие индексы

При помощи общих индексов, как отмечалось выше, чаще всего и характеризуется изменение экономических явлений и процессов.

В отличие от индивидуальных индексов их построение и исчисление является делом более сложным, этим занимается теория индексов.

По методологии расчета общие индексы подразделяются на:

• агрегатные, от латинского aggrego – присоединяю;
• средние из индивидуальных.

Основной формой экономических индексов в отечественной практике являются агрегатные. Они состоят из 2-х частей:

1. Индексируемой величины (характер изменения которой определяется).
2. Соизмерителя (веса), с которым индексируемая величина включается в общий итог.

Соизмеритель (вес) вводится в индекс для того, чтобы преодолеть несуммарность отдельных элементов изучаемого явления. Т.е. при помощи весов суммируются наборы (агрегаты) индексируемых показателей. Соизмеритель (вес) экономически тесно связан с индексируемой величиной и приводит элементы сложного явления к сопоставимому виду. Для этого веса берутся одинаковыми в числителе и знаменателе индекса.

Агрегатный индекс цен

Рассмотрим основные принципы и методы расчета агрегатных индексов на примере индекса цен и индекса физического объема товарооборота.

Если в качестве индексируемой величины выступает цена, т.е. нам необходимо определить общее изменение цен на различные товары, то чтобы преодолеть несуммарность цен следует:
– ввести в индекс соизмеритель (вес) в виде количества проданных (или произведенных) товаров.

Тогда произведение цен на количество соответствующих товаров даст стоимости этих товаров. А стоимости различных товаров уже можно суммировать.

Следовательно, в индексах цен в качестве соизмерителя (веса) индекса, выступают количества товаров. Причем, эти количества должны быть одни и те же для текущего и для базисного периода, чтобы индекс отразил только изменение уровня цен.

Таким образом, общее изменение цен на различные товары можно определить путем расчета агрегатного индекса цен введя в него в качестве веса одинаковую величину: количества проданных товаров за текущий или базисный период.

Придерживаясь принятых выше обозначений и приняв в качестве веса количество проданных товаров за текущий период, формулу агрегатного индекса цен можно представить в виде:

где p1 и p0 – цена единицы проданных товаров в текущем и базисном периоде соответственно;
q1 – количество проданных товаров в текущем периоде.

Если же принять в качестве весов данные о количестве проданных товаров в базисном периоде, то формула агрегатного индекса цен будет иметь следующий вид:

Агрегатные индексы цен, полученные по этим 2-м формулам – с текущим и базисными весами, не идентичны. Они имеют разное экономическое содержание.

Индекс Пааше характеризует изменение цен текущего периода, по сравнению с базисным, на товары, реализованные в текущем периоде.

Т.е. он позволяет рассчитать экономический эффект, который имел место при изменении цен. Изменение цен, как известно, приводит к определенному перераспределению средств в народном хозяйстве:

• от роста цен выигрывают продавцы и проигрывают покупатели;
• от их снижения – наоборот, выигрывают покупатели и проигрывают продавцы.

Индекс Ласпейреса показывает, насколько изменились цены в текущем периоде по сравнению с базисным, на товары, которые были реализованы в базисном периоде.

Т.е. он позволяет рассчитать некий условный экономический эффект, условную экономию или перерасход средств. Поэтому при расчете индекса цен используется, как правило, 1-я формула индекса с весами текущего периода, потому, что экономиста интересует не условная экономия или перерасход, а фактический экономический эффект от изменения цен.

Таким образом, чтобы рассчитать индекс цен, необходимо сопоставить стоимость товаров, проданных в текущем периоде по ценам текущего периода со стоимостью этих же товаров, но по ценам базисного периода.

Агрегатный индекс физического объема товарооборота

Если индексируемой величиной являются количества (объемы) проданных или произведенных товаров, то для того, чтобы можно было суммировать их по разным товарам – необходимо ввести в индекс количеств соизмеритель в виде цен на продукты, т.е. соизмерить количества по ценам.

Произведение количеств на цены даст стоимость (или оборот по продаже), т.е. величины, которые можно суммировать.
Следовательно, в индексах физического объема продукции, цены являются весами. Эти веса должны быть взяты одинаковыми (неизменными) для текущего и базисного периодов. В этом случае индексы отразят только изменение объемов произведенных или проданных товаров.

Таким образом, и в индексе цен, и в индексе физического объема товарооборота при помощи соизмерителей мы переходим к стоимости проданных (произведенных) товаров.

При построении и исчислении индекса физического объема товарооборота возникает вопрос: какие цены взять в качестве соизмерителя (веса)? Цены базисного, или цены текущего периода?

Чтобы агрегатный индекс характеризовал только изменение физического объема и не отражал изменения цен, в качестве весов надо взять постоянные цены как для базисного, так и для текущего периодов.

Тогда формулу агрегатного индекса физического объема продукции можно представить следующим образом:

Выбор периода взвешивания индексов объясняется тем, что качественные индексируемые показатели не требуют соизмерения и их сомножители являются только весами, а количественные – требуют соизмерения и их сомножители являются соизмерителями.

Числитель индекса представляет собой стоимость продукции текущего периода в базисных ценах, знаменатель – стоимость продукции базисного периода в ценах базисного периода. Разность между числителем и знаменателем (∑q1p0 — ∑q0p0) характеризует абсолютное изменение физического объема продукции в текущем периоде.