Уравнения четвертой степени

Алгебраическое уравнение четвертой степени:

с помощью подстановки x = z — а/4 можно привести к уравнению

в котором коэффициент при z3 равен нулю. Это уравнение можно записать так:

где а — вспомогательный параметр. Значение параметра выберем так, чтобы вычитаемый многочлен был полным квадратом. В этом случае многочлен имеет два равных корня, так как его дискриминант равен нулю, т. е.

Уравнение принимает вид

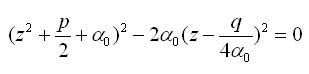
где а0 — отличный от нуля корень уравнения.

Уравнение распадается на два квадратных уравнения:

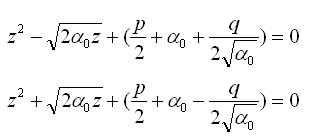
Корни этих уравнений будут корнями уравнения четвертой степени

Решить контрольные по математике Вам помогут здесь.