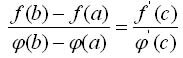Теоремы дифференцирования

Теорема Лагранжа

Если функция f(x) непрерывна на отрезке [а, b] и дифференцируема в интервале (а,b), то существует такая точка с{а,b), что

Следствие 1. Если производная функции равна нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная в этом промежутке.

Следствие 2. Если две функции имеют равные производные в некотором промежутке, то они отличаются в этом промежутке лишь постоянным слагаемым.

Корнем (или нулем) функции у = f(x) называется такое значение х = х0 ее аргумента, при котором эта функция обращается в нуль. Геометрически корень функции означает абсциссу точки, в которой график функции пересекает ось их или касается ее.

Теорема Ролля

Между двумя различными корнями дифференцируемой функции содержится по меньшей мере один корень ее производной.

Замечание 1. Теорема имеет простую геометрическую интерпретацию: между значениями а и b имеется по меньшей мере одно значение с такое, что в точке С (с, f(c)) графика функции касательная к графику параллельна оси Ох.

Замечание 2. Теорему можно сформулировать в более общем виде. Если у = f(x) — функция, дифференцируемая на отрезке [а, b] и f(а) = f(b), то
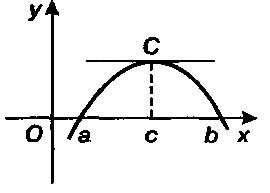
между а и b найдется точка с, в которой производная равна нулю, т. е. f'(с) = 0.

Теорема Коши

Если y = f(x) и у = у(х) — две функции, непрерывные на отрезке [а, b] и дифференцируемые в интервале (а, b) причем ф'(x) не равно 0 для любого х(а, b), то между а и b найдется такая точка с, что