Свойства определителей

• определитель не будет изменяться при замене всех его строк соответствующими столбцами;
• при перестановке двух соседних строк или столбцов определитель меняет только знак;
• определитель с двумя одинаковыми строками или столбцами равен нулю;
• множитель (коэффициент), общий для элементов некоторой строки или столбца, можно вынести за знак определителя;
• определитель равен нулю, если все элементы любой строки или столбца равны нулю;
• определитель не изменится, если к элементам любой строки или столбца прибавить соответствующие элементы другой строки или столбца, предварительно умножив их на один и тот же множитель;
• определитель равен сумме произведений элементов строк или столбцов на их алгебраические дополнения.

Например, detA = allAll+a12A12 + a13A13, т.е.

Эта формула выражает разложение определителя третьего порядка по элементам первой строки.

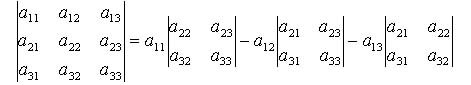
По аналогии с этой формулой вводятся определители четвертого порядка:

где А1к — алгебраическое дополнение элемента а1к, n = 4; определители пятого порядка и т. д.

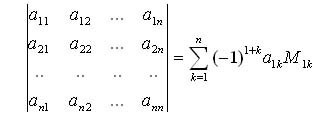
Теорема 5.1 (теорема замещения). Суммы произведений произвольных чисел bi ,b2,…,b на алгебраические дополнения элементов любого столбца или строки матрицы порядка n равны определителю матрицы, которая получается из данной заменой элементов этого столбца (строки)числами b1,b2,…,bn.

Теорема 5.2 (теорема аннулирования). Сумма, произведений элементов одного из столбцов (строк) матрицы на соответствующие алгебраические дополнения элементов другого столбца (строки) равна нулю.

Теорема 5.3. Определитель произведения двух квадратных матриц А и В одного порядка равен произведению определителей перемножаемых матриц:

Название «детерминант» предложил Гаусс. Современное изложение теории определителей дал Коши. Обозначение определителя в виде квадратной таблицы чисел с двумя вертикальными чертами ввел Кэли в 1841 г.

Рекомендуем посмотреть лекцию по теме «Матрицы», где очень доходчиво рассматриваются матрицы второго порядка

Для заказа решения задачи по математике на определители жмите сюда.