Свойства дифференциала

Основные дифференциалы

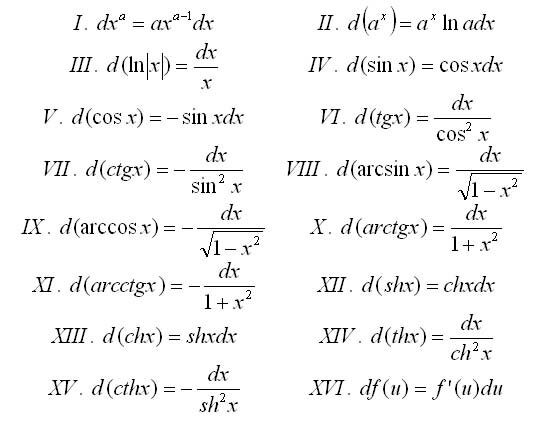
Дифференциал функции обладает свойствами, аналогичными свойствам производной.

1. Дифференциал постоянной равен нулю:dc = 0, с = const.
2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:
   d(u+v)=du + dv
   Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны
   d(u+c) = du (c= const).
3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:
   d(uv) = udv + vdu.
   Следствие. Постоянный множитель можно выносить за знак дифференциала
   d(cu) = cdu (с = const).
4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой
5. Свойство независимости вида дифференциала от выбора независимой переменной (инвариантность формы дифференциала): дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот аргумент независимой переменной или функцией другой независимой переменной.

Дифференциалы высших порядков.

Если х — независимая переменная и y = f(x) — дифференцируемая функция, то dx = f'(x)dx, т. е. дифференциал функции есть функция, зависящая от двух аргументов х и dx. Этот дифференциал будем называть также дифференциалом первого порядка (или первым дифференциалом).

Считая dx постоянной, получаем, что df(x) — функция одной переменной. Предположим, что функция у = f(x) имеет не только первую производную, но и n последовательных производных y» = f»(x), y’” = f”’(x).

Дифференциал от дифференциала функции у = f{x) называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d2y = d(dy), причем

Дифференциалом n-го порядка

Смотрите пример вычисления дифференциалов первого и второго порядков

Помощь в решении задач по математике Вам окажут тут