Ранг матрицы

Рассмотрим матрицу размером m х n

Выберем в ней произвольно s разных строк и s столбцов, причем 1 <= s <= min (m, n), где min (m,n) — меньшее из чисел m и n.

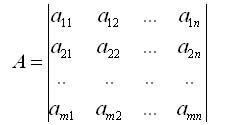
Элементы, попавшие на пересечении выбранных строк и столбцов, образуют матрицу порядка s.

Определитель матрицы называется минором порядка s матрицы А. Например, если дана матрица

то, взяв первую и третью строку, третий и пятый столбец, получим матрицу второго порядка и ее определитель

Этот определитель является минором второго порядка для исходной матрицы. Аналогично можно получить остальные миноры второго порядка и третьего порядка. Некоторые из миноров могут оказаться равными нулю.

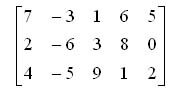
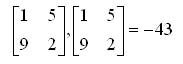
Ранг матрицы — наибольший из порядков ее миноров не равных нулю. Ранг матрицы А обозначают одним из символов: rang А, r. Если все миноры матрицы равны нулю, то ранг ее считается равным нулю.

Из определения ранга матрицы получаем следующие утверждения:

1. Ранг матрицы определяется целым числом, заключенным между 0 и меньшим из чисел m, n.
2. Ранг матрицы равен нулю, если матрица нулевая.
3. Для квадратной матрицы n-го порядка r = п тогда и только тогда, когда матрица невырожденная.

При нахождении ранга матрицы можно пользоваться свойствами миноров. Если все миноры определенного порядка матрицы равны нулю, то все миноры более высокого порядка также равны нулю. Таким образом, если среди миноров порядка k данной матрицы есть отличные от нуля, а всё миноры порядка k + 1 равны нулю или не существуют, то r= k.

Свойства ранга матрицы

1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы.

2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец.

При элементарных преобразованиях ранг матрицы не меняется. С помощью элементарных преобразований матрицу можно привести к квазитреугольной форме. Ранг квазитреугольной матрицы равен r, поскольку ее минор с главной диагональю а11а22,…,аnn равен произведению не равным нулю а все миноры более высокого порядка равны нулю (как содержащие нулевые строки).

Для решения контрольной по математике на нахождения ранга жмите сюда.