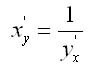Правила дифференцирования

Производная алгебраической суммы функций

выражается следующей теоремой.

Теорема 1. Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

(u±v)’ = u’±v’  

Следствие. Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

(u — v + w)’ = u’ — v’ + w’  

Производную произведения функций определяет

Теорема 2. Производная произведения двух дифференцируемых функций равна произведению первой функции на производную второй плюс произведение второй функции на производную первой, т. е.

(uv)’ = u’v + uv’  

Следствие 1. Постоянный множитель можно выносить за знак производной (cv)’ = cv’ (с = const).

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждой из них на все остальные.

Например, (uvw)’ = u’vw + uv’w + uvw’  

Производная частного двух функций

выражается следующей теоремой.

Теорема 3. Производная частного двух дифференцируемых функций определяется формулой

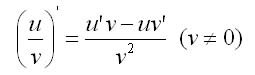
Производную сложной функции выражает

Теорема 4. Если y = f(u) и и = (ф(х)) — дифференцируемые функции своих аргументов, то производная сложной функции у = f (ф(х)) существует и равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, т. е.

Очень часто в задачах по математике на производные даются сложные функции, например, y = sin(cos5x). Производная такой функции равна -5sin5x*sin(cos5x)

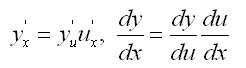
Смотрите пример вычисления сложной функции на следующем видео

Производная обратной функции

Еели у = f(x) и х = ф (у) — взаимно обратные дифференцируемые функции, то