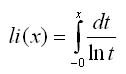Определенный интеграл с верхним пределом

Рассмотрим функцию y = f(x), интегрируемую на отрезке [а, b]. Если х на промежутке [a, b], то функция f(x) интегрируема также на любом отрезке [а, х]. Предположим, что х меняется на отрезке [а, b], тогда на этом отрезке определена функция

(Переменную интегрирования обозначили буквой t, переменный верхний предел — буквой х).

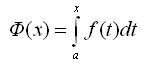
Теорема 1. Если функция у = f(x) интегрируема на отрезке [а, b], то функция Ф(х) непрерывна на этом отрезке.

Теорема 2. Если подынтегральная функция непрерывна, то производная определенного интеграла с переменным верхним пределом существует и равна значению подынтегральной функции для этого предела. т.е.

Следствие 1. Если функция f(x) непрерывна на отрезке [а, b], то при любом х

Следствие 2. Определенный интеграл с переменным верхним пределом является одной из первообразных для непрерывной подынтегральной функции.

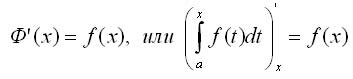
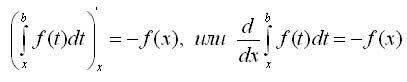
Другими словами, для любой непрерывной функции существует первообразная.

Эти функции не являются элементарными; первообразные указанных подынтегральных функций не выражаются через элементарные функции.

Все приведенные функции хорошо изучены, для них составлены таблицы значений, эти функции находят широкое применение.

Связь между определенными и неопределенными интегралами выражает следующая теорема Ньютона — Лейбница, называемая основной теоремой интегрального исчисления.

Теорема 3. Определенный интеграл от непрерывной функции равен разности значений любой ее первообразной для верхнего и нижнего предела интегрирования:

где F'(x)=f{x).

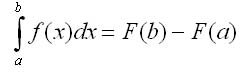
Эта формула называется формулой Ньютона — Лейбница; ее можно переписать в виде

левая часть второй формулы читается так: «двойная подстановка от а до b для функции F(x).

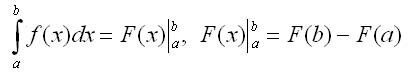
Замечание. Интеграл с переменным верхним пределом интегрирования используется при определении многих функций. К таким функциям относятся, например:

Интегральный синус

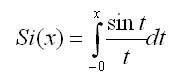
Интегральный косинус

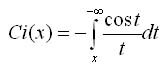
Интегральный логарифм