Определенный интеграл

Советуем посмотреть видео об определенном интеграле, или читайте информацию об интеграле чуть ниже

Пусть дана функция y=f(x), определенная на отрезке [а, b], где а < b. Отрезок [а, b] точками а = х0 < х1 < х2 < … < хn = b разобьем на n элементарных отрезков [а, х1] , [х1, ,х2],…,[xn-1, b], длины которых обозначим через дельта хk.

В каждом из элементарных отрезков [xk-1, xk] выберем произвольно одну точку кси k значение функции в этой точке умножим на длину отрезка дельта хk, получим произведение. Составим сумму всех таких произведений

Эта сумма называется интегральной суммой для функции y = f(x) на отрезке [а, b]. Обозначим через лямда, длину наибольшего из элементарных отрезков [xk-1, xk] (k = 1,2,…,n), т.е. Х = mах лямда дельта хk.

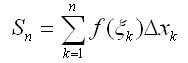
Число S называется пределом интегральной суммы S, если для любого числа е > 0 можно указать такое число б > 0, что при лямда < б выполняется неравенство |Sn — S| < e независимо от выбора точек кси на отрезках [xk-1, xk]

Определенным интегралом от функции у = f(x) на отрезке [а, b] называется конечный предел ее интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю. Определенный интеграл в задачах по математике обозначается символом

f(x) называется подынтегральной функцией, х — переменной интегрирования, a — нижним, b — верхним пределами интегрирования. Следовательно, по определению

Из определения следует, что величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е.

Функция, для которой существует предел суммы, называется интегрируемой на отрезке [а, b].

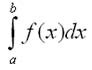
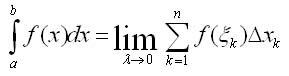
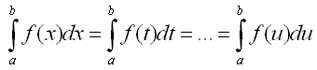
Очевидно, если ф-ция f(x) интегрируема на отрезке [а, b] то она и ограничена на этом отрезке. Обратное утверждение не верно: существуют ограниченные функции, не являющиеся интегрируемыми. К ним принадлежит функция Дирихле, равная единице в рациональных точках и нулю — в иррациональных. На любом отрезке [а, b] эта функция ограничена, но не является интегрируемой на нем.

Соответственно по определению

где f(x) — любая функция;

где f(x) — функция, интегрируемая на отрезке [b, a] (b < a). Справедливы следующие утверждения.

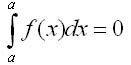
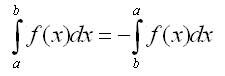
1. Если функция f(x) интегрируема на отрезке [а, b], то она интегрируема на любом отрезке [с, d], содержащемся в [а, b].

2. Если функция f(x) непрерывна на отрезке [а, b], то она и интегрируема на этом отрезке.

3. Если функция f(x) имеет на отрезке [а, b] конечное число точек разрыва первого рода, то она интегрируема на [а, b].