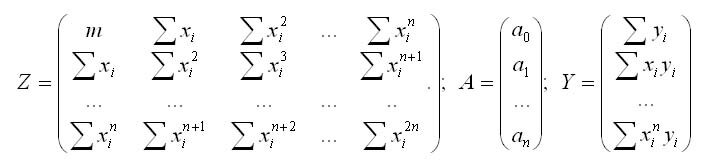Метод наименьших квадратов в математике

В большинстве экспериментальных данных, задаваемых с помощью табличной функции, имеется достаточно большой разброс точек. При этом использование кусочной или непрерывной интерполяции не всегда оправдано, поскольку ставится задача исследовать общую тенденцию изменения физической величины.

В этом общем случае аппроксимации данных искомая кривая не обязательно должна проходить через заданные точки.

Рассмотрим рис. 1, отражающий большой разброс точек. В простейшем случае будем искать аппроксимирующую функцию ф(х) в виде полинома первой степени (прямой):

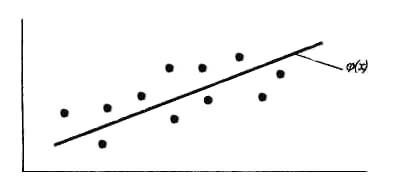
Таким образом, данная система точек группируется вокруг искомой прямой. Эту прямую легко провести на глаз так, чтобы она наиболее близко подходила к исходным точкам. Однако можно найти уравнение прямой более строгими математическими методами.

Метод наименьших квадратов наиболе часто используют для решения контрольных по эконометрике для нахождения параметров уравнений (линий, степенной функции, гиперболы и т.д.)

Пусть общее количество точек равно n.
Отклонение i-й точки от искомой прямой:

Метод наименьших квадратов заключается в минимизации суммы квадратов отклонений. В нашем случае эта функция равна

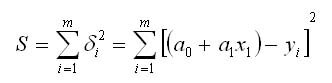
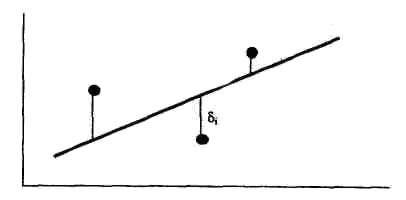
Для нахождения минимума функции S необходимо приравнять нулю ее частные производные. В результате получим систему уравнений:

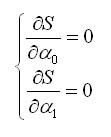
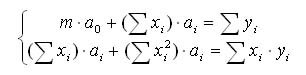
Метод наименьших квадратов несложно распространить на общий случай, когда мы будем искать функцию ф(х) в виде полинома степени n:

Неизвестные коэффициенты а находим из условия минимизации суммы квадратов отклонений искомой функции от исходных точек. По аналогии с полиномом первой степени в нашем случае имеем систему уравнений: Z*A = B

где Z — квадратная матрица размерностью (n+1)х(n+1), составленная из известных координат точек, А — вектор неизвестных коэффициентов; Y- вектор-столбец свободных членов.