Кубические уравнения

Кубическим называется уравнение:

Это уравнение с помощью формулы x = z — а/3 можно привести к виду:

Корни кубического уравнения вычисляются по формуле z = u+v (формула Кардане)

Все три корня уравнения определяются следующими формулами:

где u1 — любое из трех значений и, определяемых первой из формул, v1 — то из трех значений v, которое соответствует u на основании равенства

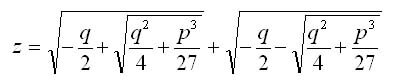
Дискриминантом кубического уравнения называется выражение

Из уравнения при D < 0 получается один действительный и два комплексно-сопряженных корня: при D = 0 — три действительных корня, причем два равных; при D > 0 — три различных действительных корня.

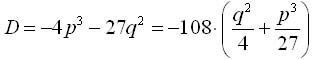
Замечание. Третий случай ( D > 0 ) называется неприводимым. В этом случае все корни уравнения с действительными коэффициентами являются действительными, однако для нахождения их по формуле z = … следует извлекать кубические корни из комплексных чисел.

Формула называется формулой Кардане. Правило, соответствующее этой формуле, впервые опубликовано в книге итальянского ученого Д. Кардане «Великое искусство или о правилах алгебры» (1545). Это правило решения кубического уравнения было получено ранее (1535) другим итальянским математиком Н. Тартальей.

Пример решения кубического уравнения смотрите ниже