Экстремум функции
Максимум функции
Рассмотрим функцию y = f(x), которая рассматривается на промежутке (а, b).
Если можно указать такую б-окрестность точки х1 принадлежащую промежутку (а, b), что для всех х (х1, б), выполняется неравенство f(x1) > f(x), то y1 = f1(x1) называют максимумом функции y = f{x) см рис.
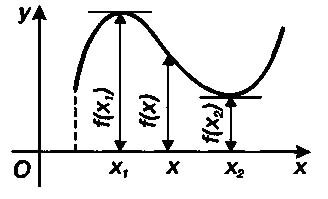
Пример нахождения максимума смотрите на следующем видео
Минимум функции
Минимум функции у = f(x) обозначим через min f(x). Другими словами, максимумом или минимумом функции у = f(x) называют такое ее значение, которое больше (меньше) всех других значений, принимаемых в точках, достаточно близких к данной и отличных от нее.
Замечание 1. Максимум функции, определяемый неравенством называется строгим максимумом; нестрогий максимум определяется неравенством f(x1) > = f(x2)
Замечание 2. Максимум и минимум функции имеют локальный характер (это наибольшее и наименьшее значения функции в достаточно малой окрестности соответствующей точки); отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции
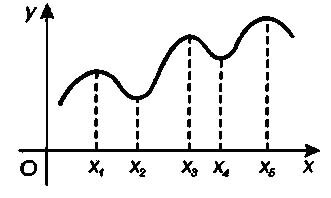
Максимум и минимум функции называются экстремумом. Экстремумы в задачах по математике находят для построяния графиков функций
Латинское extremum означает «крайнее» значение. Значение аргумента х, при котором достигается экстремум, называется точкой экстремума. Необходимое условие экстремума выражается следующей теоремой.
Теорема. В точке экстремума дифференцируемой функции и ее производная равна нулю.
Теорема имеет простой геометрический смысл: касательная к графику дифференцируемой функции в соответствующей точке параллельна оси Ох