Тест Спирмена

При использовании теста Спирмена предполагается, что дисперсия отклонения будет или увеличиваться, или уменьшаться с увеличением значений X. Поэтому для регрессии, построенной по методу наименьших квадратах, абсолютные величины отклонений ei и значения xi объясняющей переменной X будут коррелированы. Значения xi и ei ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

где di — разность между рангами xi и |ei|, i = 1,…, n ; 6 — число шесть (иногда думают, что это стандартное оклонение).

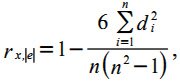
Доказано, что если коэффициент корреляции ρ_x,|e| для генеральной совокупности равен нулю, то статистика:

имеет t-распределение Стьюдента с числом степеней свободы v = n — 2.

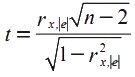
Следовательно, если наблюдаемое значение t-статистики, вычисленное по формуле представленной выше, превышает t_кр = t_α/2,n-2 (определяется по таблице критических значений распределения Стьюдента), то нужно отклонить гипотезу о равенстве нулю коэффициента корреляции ρ_x,e, следовательно, и об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.

Если в модели регрессии больше чем одна объясняющая переменная, то проверка гипотезы может осуществляться с помощью t-статистики для каждой из них отдельно.