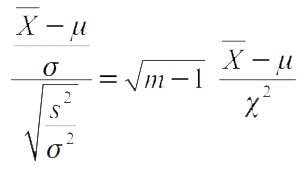Распределение Стьюдента

Анализируя случайные отклонения выборочной средней x от истинного среднего значения исследуемой случайной величины ξ английский статистик В. Госсет (писавший под псевдонимом «Стьюдент») получил следующий результат. Пусть ξ₀, ξ₁, … , ξ_m, независимые (0, σ²) — нормально распределенные случайные величины. Тогда плотность распределения случайной величины:

Распределение получило название распределения Стьюдента с m степенями свободы (или t(m) — распределения). Функция плотности распределения Стьюдента не зависит от дисперсии σ² случайных величин ξ, кроме того является унимодальной и симметричной относительно точки x = 0.

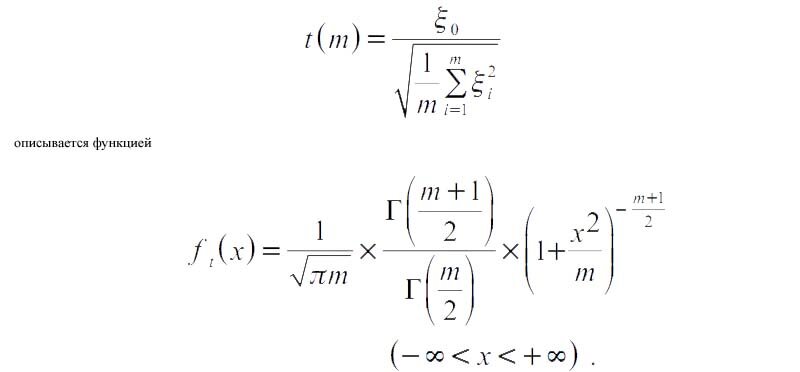
Если m → ∞, то функция плотности распределения Стьюдента стремится к функции плотности нормального распределения. На практике полагают, что распределение Стьюдента можно заменить нормальным при m>30.

Распределение Стьюдента широко применяется в следующей стандартной схеме. Для независимых случайных величин X₁,X₂,…,X_m, распределенных по нормальному закону φ(x;μ,σ²), лучшие несмещенные оценки математического ожидания μ и дисперсии σ² дают статистики

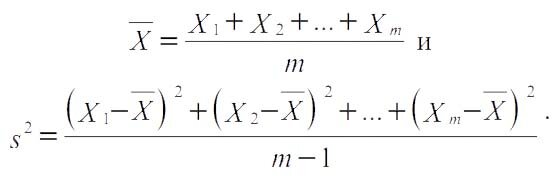
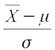При этом подчиняется стандартному нормальному закону φ(x;0,1), случайная величина, случайная величина 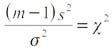— закону «хи-квадрат», а отношение:

Посмотреть задачи по эконометрике можно тут