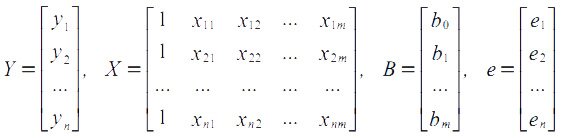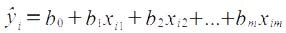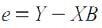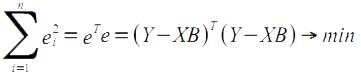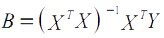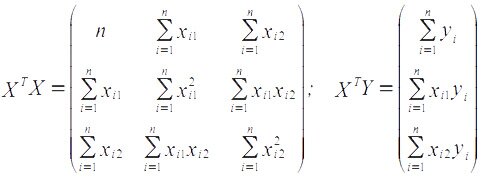Расчет коэффициентов множественной линейной регрессии матричным способом

Представим данные наблюдений и коэффициенты модели в матричной форме.

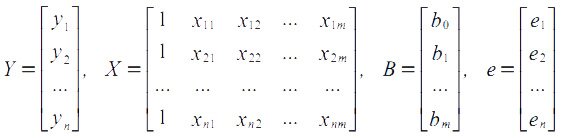
Здесь Y — n-мерный вектор-столбец наблюдений зависимой переменной; X — матрица размерности n х (m +1), в которой i-я строка i = 1, 2,…, n представляет i-е наблюдение вектора значений независимых переменных X₁, X₂,…,Xm, единица соответствует переменной при свободном члене b₀; B — вектор-столбец размерности (m + 1) параметров уравнения множественной регрессии; e — вектор-столбец размерности n отклонений выборочных значений y_i зависимой переменной от значений y_i, получаемых по уравнению регрессии:

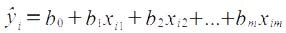
В матричном виде соотношение примет вид:

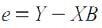
Согласно методу наименьших квадратов:

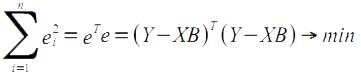
где e^T = (e₁, e₂,…, e_n), т. е. надстрочный значок T означает транспонированную матрицу.

Можно показать, что предыдущее условие выполняется, если вектор-столбец коэффициентов B найти по формуле:

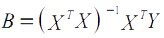
Здесь X^T — матрица, транспонированная к матрице X,

(X^TX)^-1 — матрица, обратная к (X^TX). Соотношение справедливо для уравнений регрессии с произвольным количеством m объясняющих переменных.

Пример задачи на нахождение параметров множественной регрессии

Пусть объем предложения некоторого блага Y фирмы линейно зависит от цены X₁ и заработной X₂ сотрудников, производящих данное благо. Определим коэффициенты уравнения линейной регрессии.

Матрицы имеют вид:

Таким образом, уравнение регрессии имеет вид:

Y = 95,5 + 0,818X₁ — 7,680X₂ Отметим, что в случае двух объясняющих переменных:

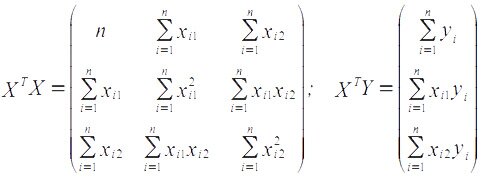
Другие примеры решения задач по эконометрике смотрите здесь