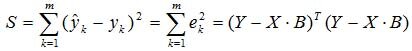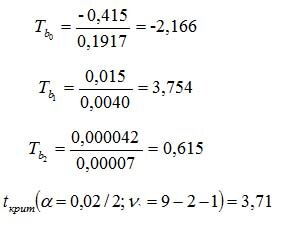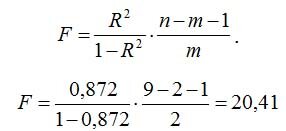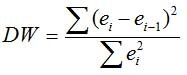Поиск параметров множественной регресии. Оценка значимости. Статистика Дарбина-Уотсона

Имеются данные по странам за 2005 год. Построить регрессионную модель:

Y= β₀  +  β₁ Х₁  +  β₂  Х₂ .

Задание.

1. По МНК оценить коэффициенты линейной регрессии _i , βi= 0, 1, 2.
2. Оценить статистическую значимость найденных эмпирических коэффициентов регрессии   b_i , i =0, 1, 2.
3. В соответствие с заданным значением  построить доверительные интервалы для найденных коэффициентов;
4. Вычислить коэффициент детерминации R² и оценить его статистическую значимость при заданном значении ;
5. Определить какой процент разброса зависимой переменной объясняется данной регрессией;
6. Сравнить коэффициент детерминации R² со скорректированным коэффициентом детерминации;
7. Вычислить статистику DW Дарбина-Уотсона и оценить наличие автокорреляции;
8. Посредством коэффициентов  b_i , i = 1, 2, оценить в % отношении влияние объясняющих переменных Х₁ и Х₂ на изменение объясняемой переменной;
9. Спрогнозировать значение объясняемой переменной Y_прогн для прогнозных значений Х_{1 прогн} , Х_{2 прогн}  и определить доверительный интервал для Y_прогн;
10. Сделать обобщающие выводы по регрессионной модели.

Страна	Индекс человеческого развития, Y	Ожидаемая продолжительность жизни при рождении 2005 г., лет, Х1	Суточная калорийность питания населения, ккал на душу, Х2
Австрия	0,904	77,0	3343
Белоруссия	0,763	68,0	3101
Греция	0,867	78,1	3575
Казахстан	0,740	67,7	3007
Китай	0,701	69,8	2844
США	0,927	76,6	3642
Турция	0,728	69,0	3568
Франция	0,918	78,1	3551
ЮАР	0,695	64,1	2933

 

Х_{1 прогн} = 73, Х_{2 прогн} =3300,   = 0,05.

1. Модель множественной линейной регрессии можно представить в виде: Y= β₀  +  β₁ Х₁  +  β₂  Х₂ .

Для определения оценок  b₀ , b₁ , b₂  воспользуемся матричным МНК. Представим данные наблюдений и коэффициенты в матричном виде:

Тогда уравнение множественной линейной регрессии второго рода запишем в виде: Y = Х В .

Остаточная сумма квадратов в данном случае равна

Результатом минимизации  является вектор:

B = (X^T X)^-1 X^T Y

Произведем операции над матрицами

Оценки вектора В являются несмещенными и эффективными, если выполняются предпосылки множественного регрессионного анализа.

Вычислим дисперсии коэффициентов регрессии   b₀ , b₁ , b₂, которые используются для оценки их точности, определения доверительных интервалов для теоретических коэффициентов  β₀ , β₁ , β₂   и  проверки соответствующих гипотез. Вариации оценок параметров будут определять и точность уравнения множественной регрессии. Для измерения их в многомерном регрессионном анализе используют ковариационную матрицу вектора оценок

Вычислим e²

2). Оценка качества уравнения множественной линейной регрессии 2-го рода определяется следующими характеристиками:
— доверительными интервалами для коэффициентов регрессии и их статистической значимостью;
— оценкой коэффициента детерминации и его статистической значимостью;
— выполнением предпосылок МНК;
— прогнозом значений зависимой переменной и его параметрами

Для проверки статистической значимости коэффициентов регрессии используется случайная величина

Тbi = bi / Sbi, i = 0, 1, 2

имеющая распределение Стьюдента.

4) Проверка общего качества уравнения регрессии.

Для этой цели, как и в случае парной регрессии, используется  коэффициент детерминации R² :

R² = 0,872

Анализ статистической значимости  коэффициента детерминации.

По величине  R² можно только предполагать насколько значимо или не значимо уравнение регрессии. Даже при небольшой величине R² (< 0,5) не всегда следует отказываться от уравнения регрессии. Для этого необходимо проверить статистическую значимость самого коэффициента детерминации. Для чего проверяются гипотезы

Н₀  :   R² = 0, Н₁  :   R² > 0.

Для проверки используется распределение Фишера. Вычисляется F – статистика:

При заданном уровне значимости  по таблице критических точек Фишера находится f_кр, и если F > f_кр , то  R² статистически значим.

Вывод: наша модель значима в целом.

5). Связь в линейной модели сильная, т.к. коэффициент  детерминации близок к 1.  означает, что вариация результата на 87,2% объясняется вариацией факторов и 12,8% приходится на долю неучтенных факторов.

7). Проверка выполнимости предпосылок МНК с помощью статистики Дарбина-Уотсона.

Статистика  Дарбина – Уотсона DW рассчитывается по формуле:

Находим критерий  Дарбина – Уотсона по формуле  СУММКВРАЗН/СУММКВ

DW = 3

По таблицам критических точек  Дарбина – Уотсона, входными параметрами которых являются: n – число наблюдений; m – количество объясняющих переменных; — уровень значимости, определяются два числа: d_l – нижняя граница;  d_u – верхняя граница.

d_l = 0,294,  d_u= 1,676

Выводы осуществляются по следующей схеме.

Если DW < d₁ , то это свидетельствует о положительной автокорреляции остатков.

Если DW > 4 — d₁ , то это свидетельствует об отрицательной автокорреляции остатков.

При d_u <  DW < 4 – d_u принимается гипотеза об отсутствии автокорреляции остатков.

Если d₁ <  DW < d_u или   4 – d_u <  DW < 4 – d₁ , то остается неопределенность по вопросу наличия или отсутствия автокорреляции остатков.

Т.к. 4 – d_u <  DW < 4 – d₁ (4 – 2,88 < 3,014 < 4 — 0,294)  мы попадаем в зону неопределенности.

9). Прогноз значений зависимой переменной

Прогнозирование мы выполнять не может, т.к. модель не значима по параметрам и также не выполняется предпосылка по критерию Дарбина-Уотсона.

Перейти на страницу выбора заданий по эконометрике можно здесь.