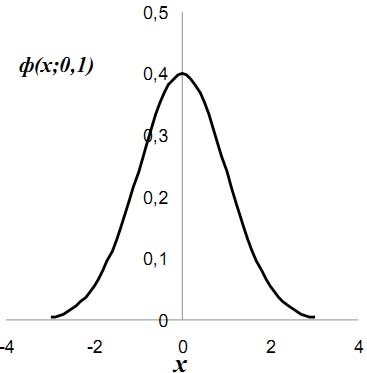
Нормальное (гауссовское) распределение

Данное распределение занимает центральное место в теории и практике вероятностно-статистических исследований. Пусть значения исследуемой непрерывной случайной величины формируются под влиянием очень большого числа независимых случайных факторов, причем сила воздействия каждого отдельного фактора мала и не может превалировать среди остальных, а характер воздействия — аддитивный.

Функция плотности случайных величин подобного типа имеет вид:

где μ и σ² параметры закона, интерпретируемые как математическое ожидание (среднее значение) и дисперсия данной случайной величины.

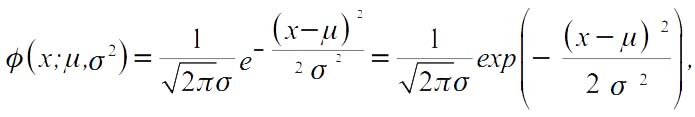
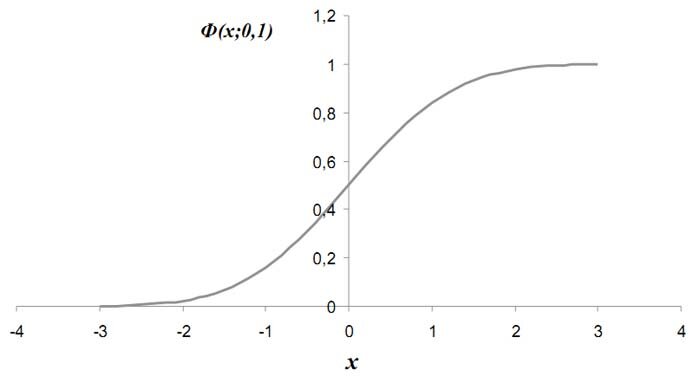
Соответствующая функция распределения нормальной случайной величины

Нормальный закон с функцией плотности

(μ = 0 и σ² = 1) называют стандартным. Во многих случайных величинах, изучаемых в экономике, технике, биологии и в других областях, естественно видеть суммарный аддитивный эффект большого числа независимых причин.

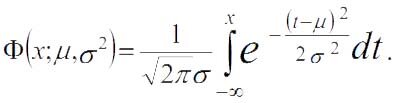
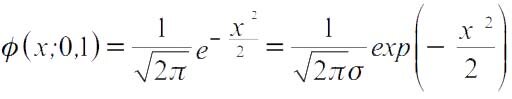
Понятие нормального закона распределения

Нормальный закон — это один из многих типов распределения, имеющихся в природе, правда, с относительно большим удельным весом практического применения. Полнота теоретических исследований, которые относятся к нормальному закону, а также сравнительно простые математические свойства делают его наиболее привлекательным и удобным в применении.

В случае отклонения исследуемых экспериментальных данных от нормального закона существует, по крайней мере, два пути его целесообразной эксплуатации: а) использовать его в качестве первого приближения; при этом нередко оказывается, что подобное допущение дает достаточно точные с точки зрения конкретных целей исследования результаты; б) подобрать такое преобразование исследуемой случайной величины, которое видоизменяет исходный «не нормальный» закон распределения, превращая его в нормальный.

Удобным для статистических задач является и свойство «самовоспроизводимости» нормального закона, заключающееся в том, что сумма любого числа нормально распределенных случайных величин тоже подчиняется нормальному закону распределения.

Рис. 1. График функции плотности стандартного нормального распределения Рис. 2. График функции стандартного нормального распределения Решение задач по эконометрике на нормальный закон распределения смотрите тут