Мультиколлинеарность

Коэффициенты интеркорреляции (т. е. сила связи между объясняющими переменными) позволяют исключить из модели регрессии дублирующие факторы. Две переменных явно коллинеарны, когда они находятся между собой в линейной зависимости, если коэффициент корреляции > 0,7.

Поскольку одним из условий нахождения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы модели коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.

Предпочтение в эконометрике отдается не фактору, более сильно связанному с результатом, а фактору, который при сильной связи с результатом имеет наименьшую тесноту связи с другими факторами. Т.е. коэффициент корреляции между факторами меньше 0,3 или, в идеале, близок к нулю. В этом условии проявляется специфика множественной регрессии как метода исследования комплексного влияния факторов на результат в условиях их независимости друг от друга.

Матрица парных коэффициентов корреляции

Пусть, например, при изучении зависимости у = f(x, z, v) матрица парных коэффициентов корреляции оказалась следующей:

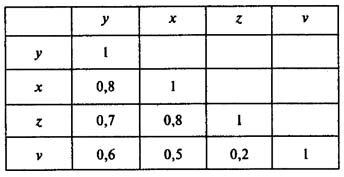
Факторы х и z дублируют друг друга, т.к. связь между ними сильная (больше 0,7). В анализ нужно включить фактор z, а не х, так как корреляция z с результатом у слабее, чем корреляция фактора х с у, но значительно слабее межфакторная связь Rzv < Rxv. Поэтому в этой задаче в уравнение множественной регрессии включаем факторы z, v

Мультиколлинеарности факторов

По величине парных коэффициентов корреляции обнаруживают только явную коллинеарность факторов. Наибольшие затруднения в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной (сильной) зависимостью, т. е. имеет место интегральное (совместное) воздействие факторов друг на друга.

Наличие мультиколлинеарности факторов означает, что некоторые факторы будут всегда действовать в синхронно. В результате вариация в исходных данных перестает быть полностью независимой, и невозможно оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).

Включение в модель мультиколлинеарных факторов отрицательно в силу следующих последствий:

• осложняется интерпретация параметров множественной регрессии как величин действия факторов, т.к. факторы коррелированны — параметры регрессии теряют экономический смысл и решение контрольной по эконометрике надо прекращать и рассматривать другие факторы
• оценки параметров ненадежны, получаются большие стандартные ошибки и меняются с изменением объема наблюдений, что делает модель регрессии непригодной для прогнозирования.

Оценка мультиколлинеарности факторов

Для оценки мультиколлинеарности факторов можно использовать определитель матрицы парных коэффициентов корреляции. Если бы факторы совсем не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной, поскольку все элементы вне диагонали были бы равны нулю. Так, для включающего три фактора уравнения

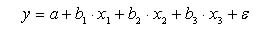
матрица коэффициентов корреляции между факторами имела бы результат, равный единице.

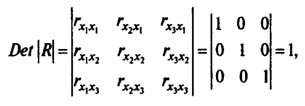
Если между факторами определилась абсолютно линейная зависимость и все коэффициенты корреляции равняются единице, то определитель (детерминант) такой матрицы равен нулю. Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. Чем ближе к единице детерминант (определитель) матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.