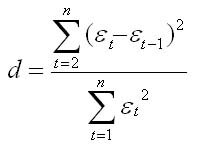Модели временных рядов. Аддитивная и мультипликативная модель
Модели, которые построенны по данным, характеризующим один объект за ряд определенных последовательных периодов, называется моделями временных рядов.
Временной ряд – это совокупность значений определенного показателя за несколько последовательных периодов времени.
Каждый уровень временного ряда может формироваться из трендовой (Т), циклической или сезонной компоненты (S), а также случайной (E) компоненты.
Модели, где временной ряд представлен в виде суммы перечисленных компонентов называются аддитивными, если в виде произведения – мультипликативными моделями.
Аддитивная модель имеет вид: Y = T + S + E
Мультипликативная модель имеет вид: Y = T * S * E
Построение модели временного ряда
- производят выравнивание временного ряда (например методом скользящей средней);
- расчитывают значения сезонной компоненты;
- устраненяют сезонную компоненту и получают выровненный ряд;
- проводят аналитическое выравнивание уровней (T и Е) и расчет значений Е с использованием полученного уравнения тренда;
- расчитывают значения T и Е ;
- расчитывают абсолютных и относительные ошибки;
Аналитическое выравнивание временного ряда
Построение аналитической функции при моделировании тренда, в любой задаче по эконометрике на временные ряды, называют аналитическим выравниванием временного ряда и в основном применяются функции: линейную, степенную, гиперболичческую, параболическую и т.д.
Параметры тренда определяются как и в случае линейной регрессии методом МНК, где в качестве независимой переменной выступает время, а в качестве зависимой переменной – уровни временного ряда. Критерием отбора наилучшей формы тренда служит наибольшее значение коэффициента детерминации, критерии фишера и Стьюдента.
Автокорреляция в остатках – корреляционная зависимость между значениями остатков за текущий и предыдущие моменты времени. Для определения автокорреляции остатков используется критерий Дарбина – Уотсона: