Идентифицируемость систем уравнений

Система линейных функций эндогенных переменных от всех предопределенных переменных системы дают приведенную форму модели:

Параметры такой приведенной системы могут быть оценены методом наименьших квадратов. Оценки, которые были полученны МНК, могут быть использованы для оценивааи структурных параметров (косвенный метод наименьших квадратов (КМНК)).

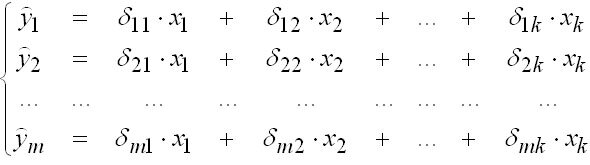
При этом возможны три ситуации:

• однозначное выражение структурных коэффициентов через коэффициенты приведенной модели – идентифицируемость уравнения;
• структурный коэффициент допускает несколько различных оценок КМНК — явление сверхидентифицируемости уравнения;
• структурный коэффициент не может быть выражен через коэффициенты приведенной модели – наблюдается неидентифицируемость уравнения.

Необходимое условие идентификации

D + 1 = H — условие означает, что уравнение идентифицируемо
D + 1 < H — неравенство означает, что уравнение неидентифицируемо;
D + 1 > H – т.е. уравнение сверхидентифицируемо

где H – число эндогенных переменных в уравнении системы,
D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе.

Достаточное условие идентификации заключается в том, что определитель матрицы, составленный из коэффициентов при переменных в исследуемом уравнении, не равен нулю, а ранг этой матрицы не менее числа эндогенных переменных системы без единицы.

Пример на идентификацию систем уравнений

Выполняя задачи по эконометрике, при решении идентифицируемого уравнения применяют косвенный метод наименьших квадратов, для решения сверхидентифицированных и неидентифицированных уравнений применяется двухшаговый метод наименьших квадратов.

Процедура косвенного метода наименьших квадратов

• составляется приведенная форма модели и определяются числовые значения параметров каждого ее уравнения обычным МНК;
• путем математических преобразований переходят от приведенной формы к структурной форме, тем самым получают численные оценки структурных параметров.

Процедура двухшагового метода наименьших квадратов

• составляется приведенная форма модели и определяются численные значения параметров каждого его уравнения обычным методом наименьших квадратов;
• выявляются эндогенные переменные, которые находятся в правой части структурного уравнения, параметры которого определяют двухшаговым МНК, и далее находят расчетные значения по уравнениям приведенной формы модели;
• обычным методом наименьших квадратов определяются параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, которые стоят в правой части данного структурного уравнения.

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.

Посмотреть бесплатно видео  по эконометрике можно здесь