Экспериментальные данные
Чтобы получить достаточно достоверные данные о распределении случайной величины, необходимо иметь выборку ее наблюдений достаточно существенного объема. Выборка наблюдений зависимой переменной Y и объясняющих переменных Xj является основой любого эконометрического исследования.
Зачастую, число наблюдений n достаточно велико (десятки, сотни) и значительно превышает число объясняющих переменных. Проблема, заключается в том, что наблюдения yi рассматриваемые в разных выборках как случайные величины Yi и получаемые при различных наборах значений объясняющих переменных Xj, имеют различное распределение. Это означает, что для каждой случайной величины Yi имеется лишь одно наблюдение. Понятно, что на основании одного наблюдения разумного вывода о распределении случайной величины сделать нельзя, и нужны дополнительные предположения.
Типы выборочных данных в эконометрике
Пространственная выборка
Пространственная выборка или пространственные данные (cross-sectional data). В эконометрике под пространственной выборкой понимают набор показателей экономических переменных, полученных в данный момент времени. Для эконометрики такое определение не очень правильно — из-за неоднозначности понятия «момент времени». Это может быть день, неделя или год. Очевидно, о пространственной выборке имеет смысл говорить в том случае, если все наблюдения получаются примерно в неизменных условиях, т. е. представляют собой набор независимых выборочных данных из некоторой генеральной совокупности. Таким образом, будем называть пространственной выборкой серию из n независимых наблюдений (p+1)-мерной случайной величины.
В вопросе определения, является ли выборка серией независимых наблюдений — нет однозначного ответа. Формальное определение независимости случайных величин, зачастую, оказывается реально непроверяемым. Обычно за независимые принимаются величины, не связанные причинно. Однако на практике не всегда вопрос о независимости оказывается бесспорным.
Пусть У — цена машины, X — год выпуска, а (X1, Y1),…, (Xn, Yn) — серия данных, полученная из газеты. Можно ли считать эти наблюдения независимыми?
Различные продавцы не знают друг друга, они дают свои объявления независимо друг от друга, так что предположение о независимости наблюдений выглядит весьма разумно. С другой стороны, продавец, назначающий цену за свой автомобиль, руководствуется ценами предыдущих объявлений в журналах и газетах, так что и возражение против независимости наблюдений также имеет право на существование.
Из вышесказанного можно сделать вывод, что решение о пространственном характере выборки в субъективно и связано с условиями используемой модели. Впрочем, то же самое можно сказать о многих предположениях, которые делаются в мат. статистике. Итак, эконометрическая модель, построенная на основе пространственной выборки экспериментальных данных выглядит так: Ух =f(Xi) + ei
где ошибки регрессии удовлетворяют условиям
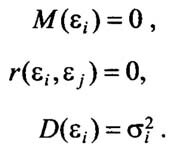
Что касается последнего условия, то здесь возможны два случая:
а) сигма квадрат i = j. Свойство постоянства дисперсий ошибок регрессии называют гомоскедастичностъю. В данном случае распределения случайных величин Yi отличаются только значением математического ожидания (объясненной части);
б) сигма квадрат i не равно j. В этом случае наблюдается гетероскедастичностъ модели. Гетероскедастичность «портит» массу результатов статистического анализа и, зачастую, требует устранения.
Как определить, является ли изучаемая эконометрическая модель гомо- или гетероскедастичной? — В некоторых случаях это достаточно очевидно. Например, цена автомобиля, которому пятнадцать лет, вряд ли может подняться выше 100000 руб., так что стандартная ошибка цены в этом случае вряд ли может быть больше, чем 15000 руб., автомобиль, которому два года, может стоить и 500000 руб., т.е. стандартная ошибка заведомо не меньше 50000 руб.
Однако во многих случаях гетероскедастичность модели далеко не столь очевидна.
Временные ряды
Временным (динамическим) рядом (time-series data) называется выборка наблюдений, в которой важны не только сами наблюдаемые значения случайных величин, но и порядок их расположения друг за другом. Как правило, упорядоченность обусловлена тем, что экспериментальные данные представляют собой серию наблюдений одной и той же случайной величины в последовательные моменты времени.
В этом случае динамический ряд называется временным рядом. При этом предполагается, что тип распределения случайной величины остается одинаковым (например, нормальным), но параметры его меняются в зависимости от времени.
Модели временных рядов, обычно, оказываются сложнее моделей пространственной выборки, так как наблюдения случайной величины в последовательные моменты времени. В этом случае динамический ряд называется временным рядом. При этом предполагается, что тип распределения случайной величины остается одним и тем же (например, нормальным), но параметры его меняются в зависимости от времени.
Модели временных рядов, как правило, оказываются сложнее моделей пространственной выборки, так как наблюдения в случае временного ряда не являются независимыми, а это значит, что ошибки регрессии могут коррелировать друг с другом.
Источник: Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов, 2002. — 311 с