Частная корреляция
Ранжирование факторов в множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии. Эту цель можно достигнуть с помощью частных коэффициентов корреляции для линейных связей. При нелинейной связи исследуемых признаков эту функцию выполняют частные индексы детерминации. Помимо этого, частные коэффициенты корреляции широко используют при решении проблемы отбора факторов: целесообразность включения фактора в модель может определяться величиной частных коэффициентов корреляции.
Частные коэффициенты корреляции характеризуют тесноту связи между результатом и фактором при устранении влияния другого фактора (или факторов), которые включенны в уравнение регрессии.
Показатели частной корреляции определяются как отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в регрессионную модель.
Частные коэффициенты корреляции, рассчитанные по рекуррентной формуле могут находиться в пределах от -1 до +1, а по формулам через множественные коэффициенты детерминации — от 0 до 1. Сравнивая их друг с другом можно ранжировать факторы по тесноте их связи с результатом.
Частные коэффициенты на основе стандартизованных коэффициентов регрессии (бета-коэффициентов) дают меру тесноты связи каждого фактора с показателем (результатом) в чистом виде. Если из стандартизованного уравнения регрессии следует, что бета 1 > бета 2 > бета 3, т.е. по силе влияния факторов на результат их порядок таков: х1, х2, х3, такой же порядок факторов определяется и по соотношению частных коэффициентов корреляции.
Для уравнения регрессии в стандартизованном виде, коэффициенты могут быть определены по формулам, исходя из решения системы нормальных уравнений:
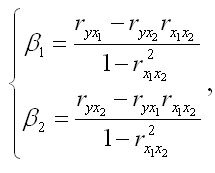

Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.