Закажите выполнение работы по статистике, математике, эконометрике или информатике у настоящих профессионалов - преподавателей университета

E-mail: [email protected]
ICQ: 617163610

Предпосылки в эконометрике

Пусть существует р объясняющих переменных Х1,..., Хр и зависимая переменная Y. Переменная Y является случайной величиной, которая имеет при заданных значениях факторов некоторое распределение. Если случайная величина Y непрерывна, то можно говорить, что ее распределение при каждом наборе значений факторов (Х1, X2, ..., Хр) имеет условную плотность fx1,x2,..., xр(y)

Как правило, предполагается, что условные распределения Y при каждом допустимом значении факторов — нормальные. Данное предположение позволяет получить значительно более качественные результаты. Впрочем, зачастую предположение о нормальности условных распределений Y приходится отвергнуть. Вместе с тем в задачах по эконометрике рассматриваются также предпосылки, что мат. ожидание случайной величины равно нулю и предпосылка об отсутствии автокорреляции остатков

Объясняющие переменные Xj(J = 1,..., р) могут считаться как случайными так и детерминированными, т. е. принимающими определенные значения. Покажем этот тезис на продажи автомобилей.

Мы можем заведомо определить для себя параметры автомобиля и искать объявления о продаже автомобиля с этими параметрами. В этом случае случайной величиной будет только зависимая переменная — цена. Но можно также случайным образом выбрать объявления о продаже, в этом случае параметры автомобиля — объясняющие переменные — тоже будут случайными величинами.

Уравнение регрессии

Классическая эконометрическая модель рассматривает объясняющие переменные Xj как детерминированные, однако, главные результаты статистического исследования модели останутся в основном теми же, что и в случае, если считать X случайными переменными.

Объясненная часть (Ye) — в любом случае будет представлять собой функцию от значений факторов — объясняющих переменных: Yе = f(Х1, X2, ..., Хр).

Таким образом, эконометрическая модель имеет вид: Yе = f(Х1, X2, ..., Хр) + e

Наиболее естественным выбором объясненной части случайной величины Y в эконометрике есть ее среднее значение — условное математическое ожидание Mх1,х2(Y), получаемое при данном наборе значений факторов Х. (Mх(Y). По своему смыслу объясненная часть (Y) — это ожидаемое значение зависимой переменной при заданных значениях объясняющих.

Уравнение Mx(Y) = f(x1,x2,..., xр) называется уравнением регрессии.

При таком естественном выборе объясненной части эконометрическая модель имеет вид Y = Mx(Y) + e
где е — случайная величина, которую также называют возмущением или ошибкой.

В курсе математической статистики это уравнение называют уравнением регрессионной модели..

Заметим, что эконометрическая модель не всегда является регрессионной, т.е. объясненная часть не всегда есть условное математическое ожидание зависимой переменной.

Систематические ошибки измерения объясняющих переменных — одна из главных причин того, что эконометрическая модель не является регрессионной.

В экономических исследованиях такая ситуация встречается достаточно часто. Одним из возможных путей устранения этого, в основном, является выбор других объясняющих переменных.

Свойства регрессионной модели

С математической точки зрения регрессионные модели оказываются существенно более простым объектом, чем эконометрическая модель общего типа. Отметим основные свойства регрессионной модели.

Рассмотрим равенство Y = Mx(Y) + e и возьмем от обеих частей математическое ожидание при заданном наборе значений объясняющих переменных X. В таком случае Мх (Y) есть числовая величина, равная своему математическому ожиданию, и получается равенство Мх(е) = 0 (а значит, и М(е) = 0), т.е. в регрессионной модели ожидаемое значение случайной ошибки равно нулю.

Можно показать, что отсюда следует (если объясняющие переменные рассматриваются как случайные величины) некоррелированность случайных ошибок и объясняющих переменных X. Это условие оказывается наиболее существенным условием состоятельности получаемых количественных результатов анализа эконометрической модели.

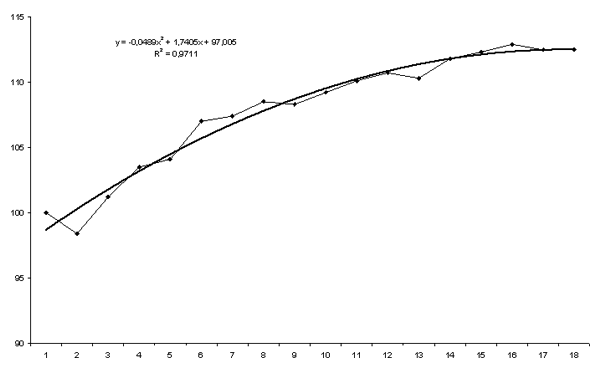Источник: Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов, 2002. - 311 с