
Модели множественной регрессии
Построение модели множественной регрессии (или многофакторная модель) заключается в нахождении уравнения связи нескольких показателей у и х1, х2 и т.д. , т.е. определяется как повиляет изменение показателей хi на величину y.
Для построения модели множественной регрессии используют:
линейную модель 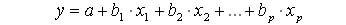
степенную модель 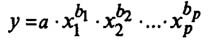
экспоненциальную модель 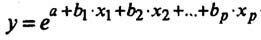
Для анализа уравнения множественной регрессии применяют метод наименьших квадратов (МНК). Для линейных уравнений, а также нелинейных уравнений, которые необходимо привести к линейным, составляется система нормальных уравнений:
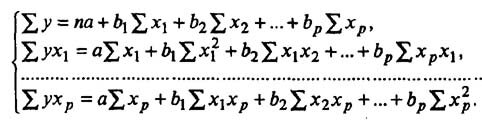
Для решения этой системы целесообразно применить метод определителей:
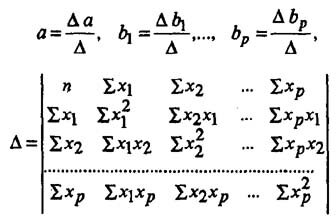
где числители в 1-м уравнении - частные определители параметров а и b, получаемые заменой соответствующего столбца матрицы определителя системы значениями левой части системы.
Другим видом уравнения множественной регрессии, которое не редко нужно находить в контрольных работах является уравнение в стандартизированном масштабе:
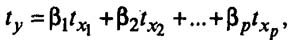
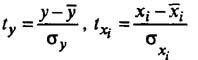
bi (бета)- стандартизованные переменные
К такому уравнению также применим МНК
Стандартизованные коэффициенты регрессии определяют из данной системы уравнений:
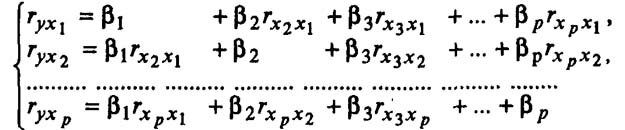
Связь стандартизованных коэффициентов с коэффициентами множественной регрессии bi в эконометрике определяются следующим уравнением
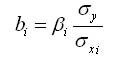
Параметр а рассчитывается по формуле
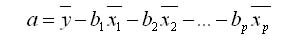
Средние коэффициенты эластичности для линейной регрессии определяют по формуле
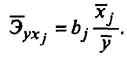
Для расчета частных коэффициентов эластичности используется формула:
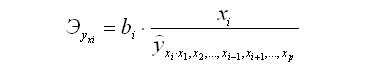
Задачи по эконометрике смотрите тут


