
Графики гетероскедастичности
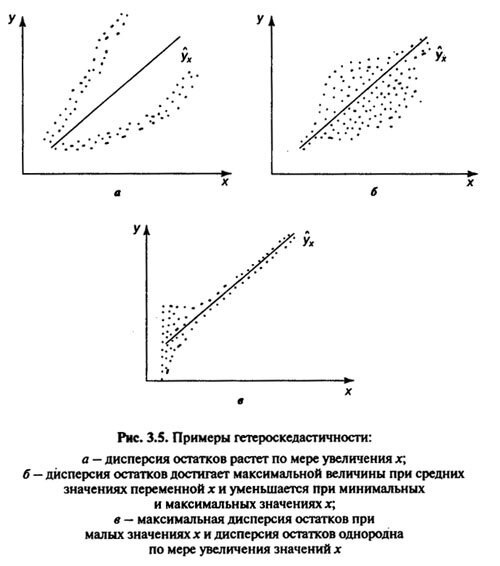
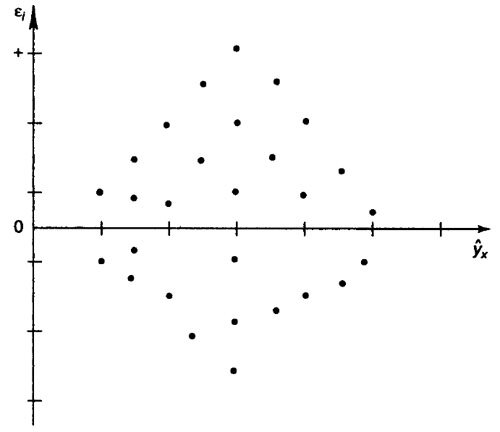
В соответствии с одной из предпосылок МНК нужно, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора X остатки е, имеют одну и ту же дисперсию. Если это условие не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно продемонстрировать на поле корреляции (см. рис.).
Гомоскедастичность остатков означает, что дисперсия остатков одна и та же для каждого значения X. Используя трехмерное изображение, можно получить следующие графики, которые проиллюстрируют гомо- и гетероскедастичность
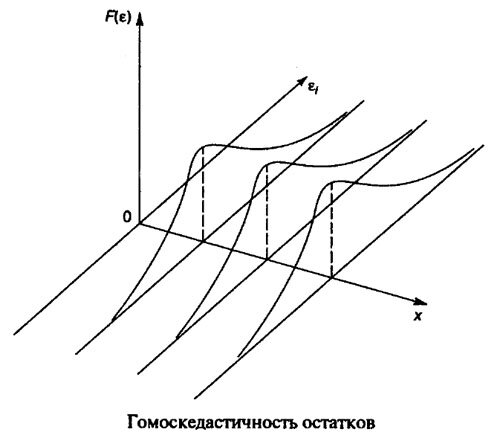
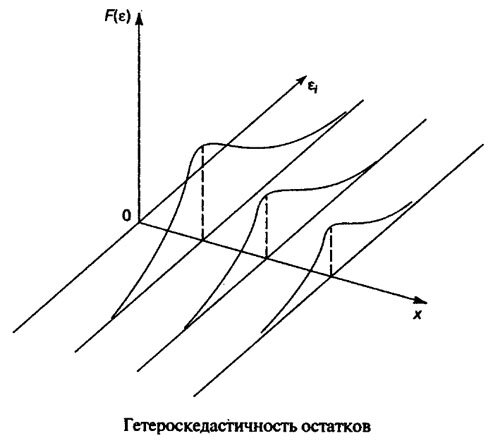
Рисунок с гомоскедастичностью показывает, что для каждого значения Х, распределения остатков одинаково в отличие от гетероскедастичности.
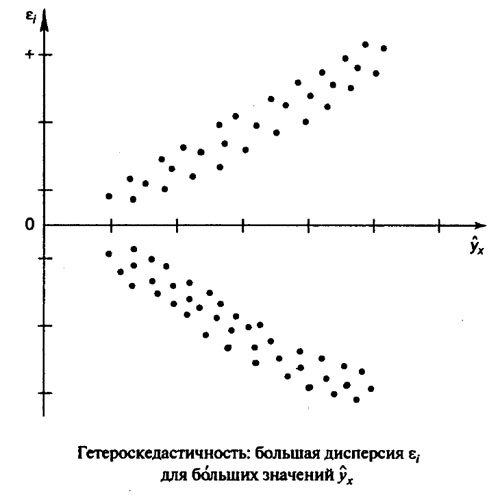
Для множественной регрессии вид графиков является наиболее наглядным способом изучения гомо- и гетероскедастичности.
Наличие гетероскедастичности может в ряде случаях привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок коэффициентов регрессии, как правило, зависит от соблюдения второй предпосылки МНК, т. е. независимости остатков и величин факторов. Гетероскедастичность будет сказываться на уменьшении эффективности оценок b. В ча-стности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии Sb, которая предполагает единую дисперсию остатков для любых значений фактора.
Определение гетероскедастичности
При малом объеме выборки, что характерно для большинства задач эконометрики, для оценки гетероскедастичости используют метод Гольдфельда — Квандта, который был разботан в 1965 г. Гольдфельдом и Квандтом, где они рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора. Чтобы оценить нарушение гомоскедастичности, они предложили выполнить следующие операции.
- Упорядочить наблюдения по мере возрастания фактора Х.
- Исключить из рассмотрения С центральных наблюдений, причем (n — С): 2 > р, где р — число оцениваемых параметров.
- Разделить совокупность из (n — С) наблюдений на две группы (с малыми и большими значениями фактора X).
- Определить остаточную сумму квадратов для первой (S1) и второй (S2) групп и нахождение отношения: R = S1 : S2.
При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять критерию Фишера с (n — С — 2p) : 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем в большей степени нарушена предпосылка о равенстве дисперсий остаточных величин.
Источник: Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М: Финансы и статистика, 2002. – 344 с.
Для перехода на страницу решения задач по эконометрике жмите сюда


