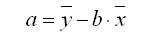Парная регрессия
Построение модели парной регрессия (или однофакторная модель) заключается в нахождении уравнения связи двух показателей у и х, т.е. определяется как повиляет изменение одного показателя на другой.
В задачах по эконометрике основным этапом является нахождение параметров модели и оценке их качества. Уравнение модели парной регрессии можно записать в общем виде:
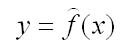
где у - зависимый показатель (результативный признак);
х - независимый, объясняющий фактор.
Линейные и нелинейные модели регрессии
Уравнение линейной регрессии: у = а + bx
Уравнения нелинейной регрессии
полиномиальная функция 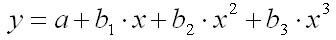
гиперболическая функция 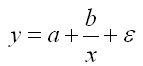
степенная модель 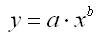
показательная модель 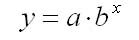
экспоненциальная модель 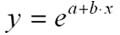
Видео лекции по моделям парной регрессии
Для более подробного изучения моделей парной регрессии советуем посмотреть это видео
Лекция 1
Лекция 2
Определение параметров в моделях парной регрессии
Нахождение модели парной регрессии в эконометрике сводится к оценке уравнения в целом и по параметрам (a, b). Для оценки параметров однофакторной линейной модели используют метод наименьших квадратов (МНК). В МНК получается, что сумма квадратов отклонений фактических значений показателя у от теоретических ух минимальна
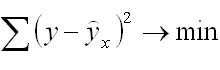
Сущность нелинейных уравнений, которые находятся в том случае, если нет линейных моделей, заключается в приведении их к линейному виду и как при линейных уравнениях решается система относительно коэффициентов a и b.
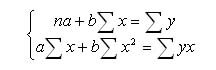
Для нахождения коэффициентов a и b в уравнении модели парной регрессии можно использовать формулы.