Линейные модели

Для того, чтобы найти объясненную часть, т. е. величину математического ожидания Мх(У), требуется нахождение условных распределений случайной величины Y. На практике это почти никогда не возможно.

В большинстве случаях при решении задач по эконометрике применяется стандартная процедура сглаживания экспериментальных данных. Эта процедура состоит из двух этапов:

1) определяется параметрическое семейство, к которому принадлежит искомая функция Мх(У) (определяемая как функция от значений объясняющих переменных X). Это может быть линейная функция, показательная функция и т.д.;

2) находятся оценки параметров этой функции с помощью одного из методов мат. статистики.

Формально никаких способов выбора параметрического семейства нет. Однако в большинстве случаев модели в задачах предмета эконометрика выбираются линейными.

Кроме очевидного преимущества линейной модели — ее относительной простоты, — для этого выбора имеются, как минимум, две существенные причины.

Первая причина: если случайная величина (X, У) имеет совместное нормальное распределение, то уравнения регрессии линейные.

В других случаях сами величины Y или X могут не иметь нормального распределения, но некоторые функции от них распределены нормально. Например, известно, что логарифм доходов на душу населения — нормально распределенная случайная величина. В большинстве случаев гипотеза о нормальном распределении принимается, когда нет явного ей противоречия, и, как показывает практика, подобная предпосылка бывает вполне разумной.

Вторая причина, по которой линейная регрессионная модель оказывается предпочтительнее других, является меньший риск значительной ошибки прогноза.

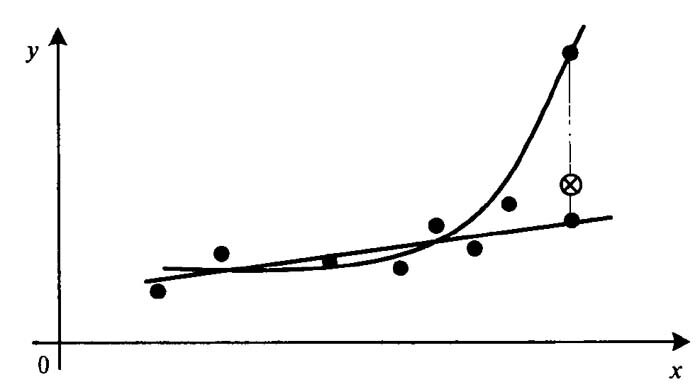
Рисунок показывает два выбора функции регрессии — линейной и квадратичной. Как видно, имеющееся множество экспериментальных данных (точек) парабола сглаживает, пожалуй, даже лучше, чем прямая. Однако парабола быстро удаляется от корреляционного поля и для добавленного наблюдения теоретическое значение может очень значительно отличаться от эмпирического.

Можно определить точный математический смысл этому утверждению: ожидаемое значение ошибки прогноза, т.е. математическое ожидание квадрата отклонения наблюдаемых значений от сглаженных (или теоретических) оказывается меньше в том случае, если выбрано линейное уравнение регрессии.

Источник: Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов, 2002. - 311 с

Видео лекции по линейным моделям

Для более подробного изучения линейных моделей рекомендуем посмотреть это видео

Лекция 1. Линейные модели

Лекция 2. Линейные модели

Заказать контрольные по эконометрике можно здесь