�� , ��

��

�� l � �� 0 �� 0� - �� 0�, �� 0 �� (�. �. �� ) �� .

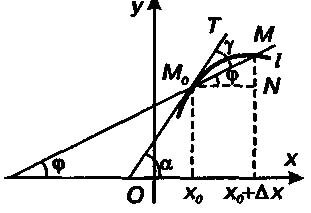
�� = f{x) � �� x0 �� �� , �� . �� = f{x) � �� 0 � �� f'(x0). ��, ��

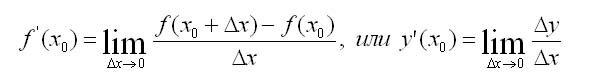
��  (� �� ) �� . �� (1797), � �� y�, f�(x), f�(x) (1770,1779). �� dy/dx �� (1675).

��

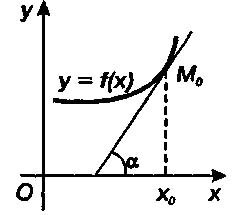
�� y = f(�) �� = x� �� (��, f(x�)), �. �.

�� ��  � �� .

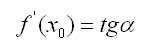
��  � �� = f(x) � �� (��, �� ) ��

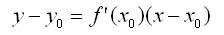
�� . �� f(x0) �� 0, �� ��  � = f(x) � �� (��, ��) �� :

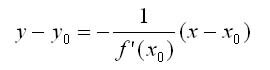
�� x = f(t) - �� , �� x� = f�(t) � �� t. ��  ��, �� �� .

�� dy/d� �� ->�0 �� (�� ), �� (�� ). �� .

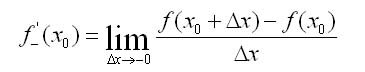
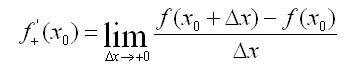
��, �� f{x) �� 0, �� f�{x) �� , �� .

��  �� : �� .

��, �� , �� . ��, �� , �� . �� , �� .

�� .

�� :
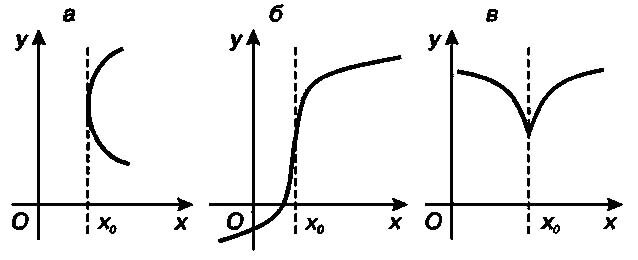