
������ ������� ���������� ���������
���� ��������� F(x)=0. ��� ����� ��� ����������� ��������� � ����� �����������. ������ ��������� �������� ����� ��� �����, �� ���� ����� �������� ��������� X, ������� ��� ����������� ���������� ��������� � ���������. ������ �� ��� ��������� �������� ������������. ��������, ���������� ��������� ���� ��^2 + b� + � = 0 ����� �������� ������������ � ����� ��� �����:
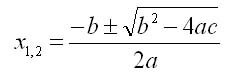
� �� �� ����� ��������� ���� ��n + b� + � = 0 � ����� ������ �� ����� �������������� �������. ��� ������� ������� ���� � ����������� ���� �^a + sinbx + x^n = �. � ����� ������, ���� ���������� ��������� �� �������� �������������� ��������, ������������� ���������� ��������� ������� � �������������� ���.
��� ������������� ��������� �������, ��� �������, �������� ���������� ����� ������� �� ���� ������:
- ��������� ������������� �������� ����� ��� ������� �� ��� �������, ��� �����������.
- ��������� ������������� �������� ����� �� ��������� ��������.
�� ������ ����� ����������� ������� ����� ��������� ������, �� ������ - ���� �� ������� ��������� (����� ����������� �������, ����� ������� ��� ����� ������� ��������). �� ����� ��� ������ �������������� ��������.
��������: �.�. �������. �����������. �������� ������-������������ ����������. �.�������� 2006
��� �������� �� �������� ����������� ����� �������� ���


