
������� ��������������, � ����
������� ������� ��������������
������� �������������� - ����� ������� �������� ��������, ��� ���������� �������� ����� ����� �������� � ������������ ����������� ����������. ��� ���� ����� ��������� ������� ��������������, ���������� ����� ���� �������� ��������� ��������� �� �� �����.
��� ����������� � ��� �������, ����� ����� ������������ �������� ��� ���� ������������ �������� ������ �������� ��������� ��������� �� ������. �������� ������� �������������� ����� ������� ����� ���� ���������� ����� � ��� ����� ���������� ���� ���� ����������.
������� �������������� ����� ���� ��������� �� �������:
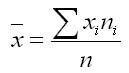
��� n � ����������� ������������.
�������� ����� �� ���������� ������� �������������� ��������
���� ������� �������������� ��������
������� �������������� �������� ������������ � ����� ������� ������� � ���������� �������. ������� �������������� ������� ����� ������� ����� �������� ������ �������� ������������ ��������, ����������� �� ����� ����� ���� ��������. � ��������� ����������� �� ���������� ��� ������������ �����, ����� ������� ����������������� �������������� �������� ��������, � ����� ���� ��������� �� �������:
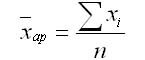
��� n � ����� ����������� ������������ �������� �.
������� �������������� ���������� � ��� ������� �� ���������, ������� ����������� ������ ����� ��� ��� ����� ��������� ���. ��� ����� ���� ���������� �� �������:
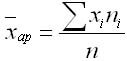
�������� �������� ������� ��������������
- 1. ���� �������������� �������� �������� (��������), ��������� (���������) � n ���, �� ������� �������� ������ �������� �������������� ���������� ��� ���������� �� ������� ��.
- 2. ���� ��� �������� ������������ �������� ��������� (���������) �� ����� �, �� ������� �������������� �������������� ��������� �� ��� �� �����.
- 3. ���� ��� ���� ����������� ��������� ��������� (���������) � k ���, �� ������� �������������� �� ���������.
- 4. ����� ���������� ��������� �������� �������� �� ������� �������������� ����� ����.
����� ���������� ��������� ������� �� ��������� ������� ��� �� ������� ��������� ������ ������������. ��������, ������� ����������� � ������ ������������ ����� ������� �� ������� ����������� �� ��������� �������� ������. ������� �� ������� ������������ ��� ��, ��� � ������� �� �������������� �������� ��������.
��������: �������� B.C. ���������� � �������� � �������: ����. �������. � �.: ��. �����, ���-�� ��������, 2004. � 344 �.


