
������ ������� ������ �������� ���������
� ������� ������ �������� ��������� �������� �������������� ������ �� ����������. ���������� ���������� ������.
���� ������� n �������������� ��������� � n ������������:
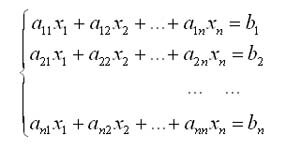
��� ������� ����� �������� � ��������� ����: � � X = �, ���
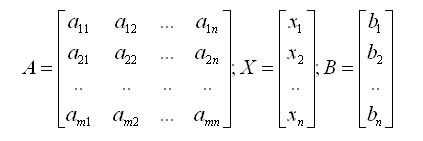
� - ���������� ������� �������������, X - ������-������� �����������, � - ������-������� ��������� ������.
��������� ������ ������� ������ �������� ��������� ������� �� ������ � ������������.
������ ������ ���������� �������� ����������� ��� ���������� �����������. ��� ������ ������������ ������ � �������� ��� �������� ������ ������.
����������: ������� �������� � ������ ��� ����� ���� ������� �. ��� ������� �������� ������� ����������� ����� ����� � ������ � ������������� �������������� �����������. ����� ����, ����������� ���������� ����� ���������� ������� X. ������� ������ ������ ������ ��������� ��� ��������� �������� ������� (n < 200).
������� ������ ������� ������� ������ �������� ���������
����� ������������� �������, ����� ������. ������ �� ��� ����������� ������ �����, ��� ��� � ������ n �������� ���������� ������������� ����� ����������.
������������ ������ �������� �� ���������������� ������������. �������� ��������� ������������ �������� ������� � - ��������� �����������. ����� � ������� ���������� ��������� ���������� ������ ���� ���������� - ��������, � ���������� �������� ���������� ����� ����������� ������� �. �������� ���������� �� ��������� ������� � �������� ���������.
�������� ������� ������ �������� ��������� ����� ����� ������, ��� � ������ �������. �� ������ ����������� ������� ����������. ������ � ���� ������� ������������ ������ ����������������. ��� ������� �������� � ������ ��� �� ���� ������� A, � ���� ���������� ��������. �������������� ����������� ����������� �� �������������. ������� ������������ ������ ��������� � ��� ������� �������� �������. ������� - ����� ������� �������� � ����� �������.


