
������������ ������� � �������� �������
������������� ���������� ������� ������� �������:
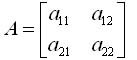
���������� �����, ������ �11�22��21�12 � ������������ ��������
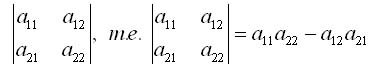
����� �11, �12, �21, �22 ���������� ���������� ������������ ������� ������� �������. ������ ������� ������������ ��������� ������ � � ����� ���������; ������ (1) ���������� ����� ������, ������ (2) - ����� �������, �� ����������� ������� ��������� ��������������� ������� (��������, ������� �21 ����������� ������ ������ � ������� ������� ������������).
������������ ������� �������� ����� �������������. ��� ������������ ������� � ����������� �� ���������� ������������� ��������� �����������:
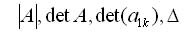
�������� ���������� ���������, �� ����� �������� ������ �� ���� "�������"
������������� ���������� ������� �������� �������

�������� �����
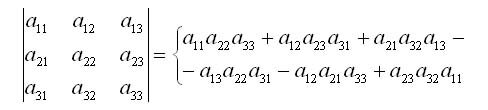
�������, ��� ������ ��������� �������������� ����� � ������ ����� ���� ������� ������������ �� ���� ������������ ��������� ������������, ������ �� ������ �� ������ ������ � ������� �������. ����� ������������ ������������� ��������������� ����. ����� ���������, ����� ������������ ������� ����� �� ������ ����, ����� �� ������ �����, ������� �������
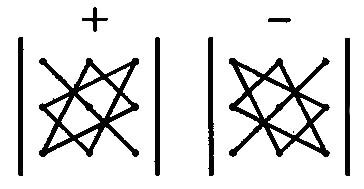
������� ������ �������� ������� (������������) ���������� ������������, ������� ������� �� ������� ������������� ��� ������ � ���� �������, ������� ����������� ������ �������. ����� �������� �ik ��������� �ik.
�������������� ���������� �������� �ik ������� - �����, ������ �� ������ (�1)^(i+k). �������������� ���������� �������� �ik ����� ���������� ����� �ik. � ������������ � ������������ Aik=(-1)^(i+k)*Mik.
������������ ������ ������� ������� � �������� ������� ���� �������� �������������� ������� � �������� �������.


