������ �� �����������

�������� �������������

��������, detA = allAll+a12A12 + a13A13, �.�.

����������� �������

��� ������� �������� ���������� ������������ �������� ������� �� ��������� ������ ������.

�� �������� � ���� �������� �������� ������������ ���������� �������:

������� n-�� �������

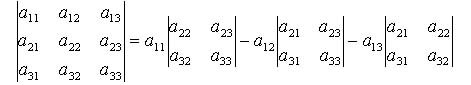
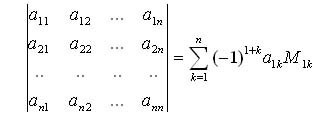
��� �1� - �������������� ���������� �������� �1�, n = 4; ������������ ������ ������� � �. �.

������� 5.1 (������� ���������). ����� ������������ ������������ ����� bi ,b2,...,b �� �������������� ���������� ��������� ������ ������� ��� ������ ������� ������� n ����� ������������ �������, ������� ���������� �� ������ ������� ��������� ����� ������� (������)������� b1,b2,...,bn.

������� 5.2 (������� �������������). �����, ������������ ��������� ������ �� �������� (�����) ������� �� ��������������� �������������� ���������� ��������� ������� ������� (������) ����� ����.

������� 5.3. ������������ ������������ ���� ���������� ������ � � � ������ ������� ����� ������������ ������������� ������������� ������:

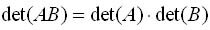
�������� ������������ ��������� �����. ����������� ��������� ������ ������������� ��� ����. ����������� ������������ � ���� ���������� ������� ����� � ����� ������������� ������� ���� ���� � 1841 �.

����������� ���������� ������ �� ���� "�������", ��� ����� ��������� ��������������� ������� ������� �������