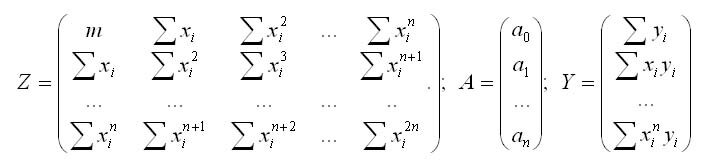����� ���������� ���������

� ����������� ����������������� ������, ���������� � ������� ��������� �������, ������� ���������� ������� ������� �����. ��� ���� ������������� �������� ��� ����������� ������������ �� ������ ���������, ��������� �������� ������ ����������� ����� ��������� ��������� ���������� ��������.

� ���� ����� ������ ������������� ������� ������ �� ����������� ������ ��������� ����� �������� �����.

���������� ���. 1, ���������� ������� ������� �����. � ���������� ������ ����� ������ ���������������� ������� �(�) � ���� �������� ������ ������� (������):

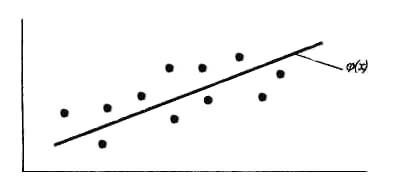
���. 1. �������������

����� �������, ������ ������� ����� ������������ ������ ������� ������. ��� ������ ����� �������� �� ���� ���, ����� ��� �������� ������ ��������� � �������� ������. ������ ����� ����� ��������� ������ ����� �������� ��������������� ��������.

����� ���������� ��������� ������� ����� ���������� ��� ������� ����������� �� ������������ ��� ���������� ���������� ��������� (�����, ��������� �������, ��������� � �.�.)

����� ����� ���������� ����� ����� n. ���������� i-� ����� �� ������� ������:

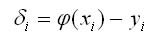
��� ����� �� ���. 2, ���������� ����� ���� ��� ��������������, ��� � ��������������. ������� ��� ����, ����� ���������� �������� ������� ������� � ��������� ������, ���������� ��������� ����� ��������� ���� ����������.

����� ���������� ��������� ����������� � ����������� ����� ��������� ����������. � ����� ������ ��� ������� �����

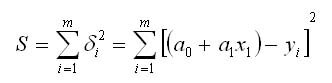
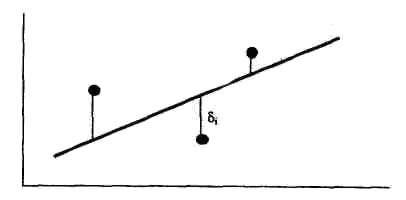
���. 2. ������ ����������

��� ���������� �������� ������� S ���������� ���������� ���� �� ������� �����������. � ���������� ������� ������� ���������:

������� ������������� ��������������, ������� ������� ��������� ��� ���������� ����������� �������������:

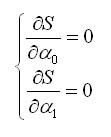
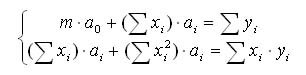
����� m - ���������� �����; ������������ ����� � ����� �������������� �� ���� ������.

����� ���������� ��������� �������� �������������� �� ����� ������, ����� �� ����� ������ ������� �(�) � ���� �������� ������� n:

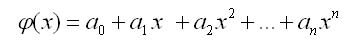
�������, ��� � ������ ������������� ������ ����������� ��������� �����������, ����������� ���������� �������� ����� m � ������� �������� ��������:

������ � ������ ��������� �� �������� � ������������ (��� ���������� ����� ����).

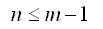
����������� ������������ � ������� �� ������� ����������� ����� ��������� ���������� ������� ������� �� �������� �����. �� �������� � ��������� ������ ������� � ����� ������ ����� ������� ���������: Z*A = B

��� Z - ���������� ������� ������������ (n+1)�(n+1), ������������ �� ��������� ��������� �����, � - ������ ����������� �������������; Y- ������-������� ��������� ������.