
�������� �����������, ����������� � �������� �������
����������� � ����������� ������� ����������� ������� � = f(x) ���������� ���������� �' = 0
������� � = f(x) ���������� ������������ � ���������� (�, b), ���� ��� ����� ���� �������� x1 � �2 �� ����������� x1 < x2 ������� ����������� f(x1) < f(x2)(�).
������� � = f(x) ���������� ��������� � ��������� ����������, ���� ��� ����� ���� ��������, ������������� ����� ����������, �� ����������� �1 < �2 ������� ����������� f(x1) > f(x2) (�).
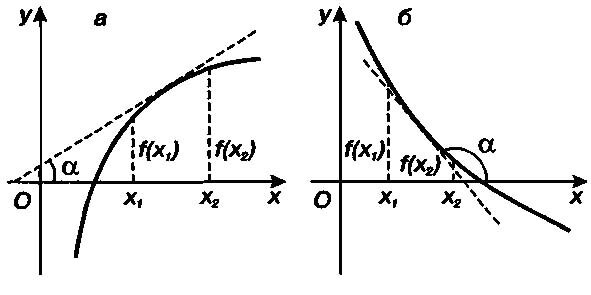
����������� ������� ����������� ��� �������� ������� ���������� ��������� ��������.
������. ���� �� ������ ���������� ����������� ������������, �� ������� ���������� � ���� ����������; ���� ����������� ������� ������������, �� ������� �������.
���������. ������� ����� ������� �������������� �����. ���� � ��������� ���������� ����������� � ������� ������� � = f(x) �������� � ���� �� ������ ���� a (tg � > 0), �� ������� ���������� � ���� ���������� (�). ���� ����������� � ������� �������� � ���� �� ����� ���� a (tg � < 0), �� ������� ������� (�).
��� �������� �� �������� ����������� ������ ������� ����


