
��������� � ������ ���������
�������� � �����������, ���������� ��������� ������ ����� ������ �� ���.

���������� ��������, ���������� ��������� ������ ��� Oz ������ �����, �������� ���������������� �����������
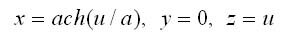
��� ����� ����������� � ��������� Oxz. � ������������ � ��������������� ���������� ����������� �������� ������� ��������������� ��������� ���������
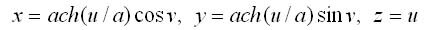
�������� �� ���� ��������� ��������� u, v, ��������
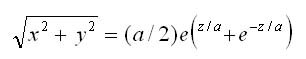
�������� �������� ������������ ����������� ������������ ����� ������������ ��������. ����������� ����������� �������� ��� ������� ��������� ������: ����� ���� ������������, ���������� ����� ������ ��������� ���������������� �����, ����� ��, ������� ����� ����������� ������� �����������, ������������ ������ ������. ������ ���������� � �������� ����� �����������. ����������� ����� ����� ��������� ������� ����������������� ������ ��������� ����������� ������������ ����������� ������� ������, ��������� �� ����������� ������.
�������� �������� ��������� ���������. ���������� ��� ����������, ���������� ������������ ��������� �������������� ����������� z = - �, z = �. ����� �����������, ���� ������� ��������� � ����� ������������, ����� ������� �������, ��� ����� ���������, ������������� ����� ���������� ������������. ������� ������, ����������� ������ ���������� ��� ��������� ��� ����������� ���������, ��������� ����� ���������.


