
��������� � ������ ��������� (�����������)
�������� - �����������, ��������� ������, ������� ��������� � ���������� ������� ��������� ������ ����������� ���, ���������� ��� ��� ���������� ����� � � ������������ ������������ ������������� � ���������� ��������� ����� ���� ���. ��� � = 90� �������� �������� ������ (�), ��� � �� ����� 90� �������� �������� ����� (�).
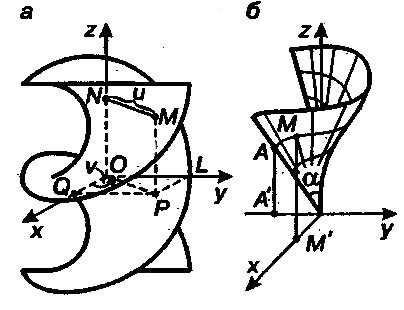
���������� ������ ��������, ��������� ������, ���������������� ��� Oz (�). ����� M{x,y,z) - ������������ ����� �����������, �- �� �������� �� ��������� ���, Q,L- �������� ����� � �������������� �� ��� ��, ��. ��������� ����� � ���������� ����� � �� ��� Oz (/MN / = /��/ = u), � ����� v - ����, ���������� �������� �� � ���� ��.
��������������� ��������� ��������� ����� ���
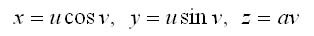
��� � � ��������� ����������.
��������� ������������� � ��������� ��������� ������ (�����) ��� v = const ���� ������� �������� ��������.
������������� � ��������� ����� ���������, ��������, �������� �������� ����� ��������� ��� ��� ������������ ������. �������, ��� ������������� ��������� �������� �������������, ������������. ������ ����� ����������� ��� ��������� ��� �������� �� �����.
������������� ��������� ������ ����������� �� ��������. ��� ����������� ���������: �������� ��������� ��������� ���� ����� ���������������� ����� ������������ �������� � �������������� � �������������. ���������� ����� �������� ����� ��������� ���, ��� ���������� ������� �� ������ �� ��������� ����� �������� � �������, ��� ����� ����� ����������� � ����� ������.


